Cite as in
K.Pribram, ed, Origins: Brain and
Self-Organization,
Additional comments since publication appended to the end. (See the book for the actual figures.)
The Brain as a Neurocontroller:
New Hypotheses and New
Experimental Possibilities
Paul
J. Werbos
Room
675, National Science Foundation*
This paper will describe how
a new body of mathematics -- initially motivated by neuroscience but developed
in recent years through engineering applications -- can begin to yield a predictive,
empirical understanding of the phenomenon of intelligence in the brain.
The paper is mainly written for neuroscientists, or for engineers working with
neuroscientists; it tries to describe crucial new experiments which need to be
performed in order to test and refine this new understanding.
The biggest single obstacle to the full use of
mathematics in real neuroscience is the sheer difficulty of the relevant
mathematics. The brain is far more complex than today's computers; therefore to
understand it, one must use even more sophisticated mathematics than the
average research engineer is familiar with. Because of this difficulty, a few
"middle men" have presented oversimplified description of biology to
the engineers, and oversimplified descriptions of the engineering to the
biologists. These oversimplifications have often led to considerable
misunderstanding and justified mistrust.
Because of these communications problems, this paper
will be written in an extremely informal style. It will consist mainly of the
transcript of a one-hour talk, edited for readability, with a few critical
updates inserted. The first section will explain the fundamental approach, and
move directly to the "bottom line" -- to some specific areas where
new experiments are badly needed. The next two sections will discuss the
underlying theory and mathematics in more detail. The second section will
discuss the issue of supervised learning, which can shed light on local
circuits within the brain. The final section will discuss the major
concepts of neurocontrol, which can shed light on the global organization
which unifies these local circuits into a truly intelligent system.
INTRODUCTION
AND OVERVIEW
Goals of This Talk
I really am grateful to
speak for once to an audience that is said to have a lot of physiologists in
it. I wish I had more chances to do this, because I think that some of the
things that we've learned on the engineering side lead to some very interesting
experimental possibilities on the physiological side; if we had more chances to
talk to each other, we could learn a lot more about experiments which nobody is
doing which could lead to some very exciting results in the future. That is
what I would really like to talk about today.
_______________________________________________________________________________
*The views herein are those
of the author, not those of NSF; however, as government work, it is in the
public domain conditional upon proper citation. This is an updated version of a
paper in Computational Neuroscience
Symposium 1992, edited by M.Penna, S.Chittajalu and P.G. Madhavan,
available from Madhavan at the Electrical Engineering Department at IUPUI in
Now, because it is late in the day, I figured it
might be useful for me to summarize everything I am going to say in one list,
so that you can see that it is finite, anyway. I'm basically going to try to
make four major points today:
(1) First, I'm going to
argue that we can understand intelligence or the brain in the same kind of
mathematical way that we understand
physics, as a real science. I'm not saying we're there yet, but I think it can
be done.
(2) Second, I'm going to
argue that neurocontrol gives us new mathematics, which is the mathematics we
need in order to understand the brain
mathematically.
(3) I'm going to argue that
neurocontrol has made enormous progress in the last few years, in terms of
new engineering applications, new
mathematical designs and ideas, and new links to the brain. Jim Bower has described this process as a
kind of convergent evolution. If you
look at the simple‑minded neural nets you see in a lot of the neural net
conferences, they don't have much connection to biology. But when you look at
people who have to solve really difficult, hard engineering control problems,
they're driven to some of the same complexities
we observe in the brain. So I would
argue concretely there are signs of convergent evolution.
(4) Finally, most important,
is that what we now have learned about what the brain might be doing suggests
new opportunities for experiment. It suggests some surprising predictions. If
the predictions are right, then you can use
experiments to surprise a lot of people and have fun changing the culture, and
if they're wrong, you can surprise a lot of mathematicians and come up with
some new computational principles that people think are impossible. So either
way, it's really important.
A caveat here is that as an
NSF program director I'm not telling you that I've got a lot of money for this.
In fact, I'm not allowed to spend money on things other than neuroengineering;
my present budget is too small to allow anything more. I think that this is a
very unfortunate situation, because if we're going to try to understand the
human mind and human learning -- subjects of truly enormous importance -- then
we have got to bring these things together; but right at the moment, there's
essentially zero dollars available for the specific kind of two-way cooperation
I'll be talking about today. I really wish somebody could fix that. (As this book goes to press, The Biology
Directorate at NSF is preparing a Collaborative Research Initiative which could
help fill this vacuum; however, the exact role of Engineering in that
initiative is not yet clear.)
If this were an audience of policy people, or people
who talk to their congressman, I would spend ninety percent of my time up here
on items number one and two on my list.
I could spend a good hour on this
-- on the theory and the philosophy and all of that. If this were an
engineering audience, I would talk about the applications and the designs; I have
done that for about eight hours at a stretch.
But here I am going to try to jump ahead to the brain stuff, but this is
a little risky. You have to bear in mind
that the kind of mathematics that's relevant to the brain is not the easy
stuff. The kind of math you can totally
understand in twenty minutes‑‑that isn't what relates to the brain.
The brain is a little more complicated, so I'm going to have to jump over some
stuff and give some citations.
Can we Understand the Brain Mathematically?:
Prospects for a Newtonian Revolution
Before I get going, though,
I really do want to say a little bit about the generalities here.
I suspect that a lot of the people in neuroscience
started out by wanting to understand the human mind. They really wanted to understand something
fundamental and important. But then they ran into a problem. Do you remember
the old saying:"When you're up to your knees in alligators, it's hard to
remember that your goal was to drain the swamp."? All of us have that problem, from time to
time. I suspect that a lot of neuroscientists discover, as time goes on, that
the brain is so complex that they lose hope of figuring it out in their own
lifetimes. Some
people have made a formal
philosophy of that; they say, "look, the information content in any one
brain is more complex than what I have spare neurons to understand, so by
definition I cannot understand another brain, let alone everybody's brain."
But let us think about that idea a little more
carefully.
If you try to know all of the synapse strengths, the
connections, the state of all the networks in somebody's brain, and the
reverberatory dynamics -- then of course, that is too complicated to ever
understand in your life. There is no way that all of those details can be fully
known scientifically. There will always be lots and lots of islands of
understanding, and those islands are useful.
We've seen good examples of studying connections even here today. But
they don't tell you how intelligence works as a whole system. They're just
little islands. And that is very
discouraging.
But think back, how did physicists solve this
problem, how did physics become a science? Basically there was this guy Isaac
Newton, and what did he do? Instead of trying to describe every physical object
in the universe, physics gave up on that, and they said "let us try to
understand instead the simple underlying dynamics which change all of
that complicated stuff over time."
Maybe all of these complicated things are governed by something simple
enough you can understand it. In
physics, "simple enough" meant a page of equations and a thousand
pages of explanation -- not trivial, but understandable.
My argument is that the same kind of approach could
work on the brain if you think of learning as the dynamics. There is every reason to believe that
underneath the complexity in the cerebral cortex and so on, there is a
generalized, modular plasticity. Lashley has shown this, and I've heard of
recent experiments where they've trained linguistic cortex to develop edge
detectors just by wiring it up differently. It's very clear that there is a
uniform, generalized modularity there in the interesting parts of the brain,
which ought to be understandable if we focus on the learning, the plasticity[1].
Knowing the laws of learning would not immediately tell us a lot of specialized
things about how we process specific sensory inputs in specific ways, but
physicists have found that if you understand the underlying dynamic laws that
control everything else, that's incredibly important later on when you try to
do engineering.
So let us try to see if we can create ‑‑
I think we can create, in principle -- a Newtonian revolution, by focusing on
the basic laws of learning in the high‑level, modular organs like
the cerebral cortex, the limbic lobes,
the cerebellum, the olive, and so on. We won't ever understand the motor pools
that way; they're like ad hoc preprocessors and postprocessors. But the really
important stuff we can understand, in principle.
But of course you can't do that unless you have the
right math.
I'll talk more about these issues later on, when I
discuss recent progress in neurocontrol.
Neuroengineering and Neuroscience:
What is the Basis for Collaboration?
Let me move ahead now to the
first slide (Figure 1 on the next page).
This is again a generality slide.
Like everybody else here I'm arguing that we need interdisciplinary
cooperation, but I'd like to say a little bit about where the problem is,
because we need to do more than just say
interdisciplinary cooperation is needed; we need to have a concrete
image in our heads of what it's about, or else we'll never be able to implement
it.
A lot of people are excited because folks in the
neuroscience side of the world studying the brain are now using neural network
models. They are building up the field
of computational neuroscience, which still belongs on the left-hand side of
Figure 1. In computational neuroscience,
we describe the brain by use of differential equations or other
mathematical models, instead of just verbal anecdotes and whatnot. That's exciting. On the right-hand side of figure 1, in
neuroengineering, we are using neural network systems to solve real‑world
engineering problems; that's also very exciting.
Figure
1. An NSF Definition of Neuroengineering
But the problem is this: what is the connection
between the left and right sides of Figure 1?
Even in today's symposium, which is very interdisciplinary, it is pretty
easy to classify most of the talks into who is doing computational neuroscience
and who is doing engineering applications.
It's like a gulf. And what's the problem? What's
happening is that we're both using neural network models, but one group is
using as its standard of validation: "Does the model fit the low‑level
circuit and the empirical data down at the low‑level circuit?" Maybe more than that. But in engineering, the test is: "Does
it work?" So we have two different
communities, based on two different standards of validation. But in reality, the brain itself meets
both tests. The real circuits not
only fit their own biological data, they also work in solving very complex
control challenges. Instead of having
two communities, using two different standards of validation to inspire and to
evaluate their work, we need to think of using both standards of validation
together. And that's how we can get
feedback back and forth here. I won't elaborate on this today; this is just a
matter of general principles. As I said before, unfortunately, my tiny bit of
money is entirely on the neuroengineering side, and that's something that needs
to be changed.
Neural Nets and Neurocontrol:
Where Is the Right Mathematics?
A lot of people are worried
that the artificial neural network (ANN) community, the engineering community,
is itself caught in a kind of local minimum. It is true that 90% of the papers
you see in a neural network conference these days talk about pattern
recognition, and what are they actually doing?
Usually, they are doing pattern classification, using associative memory
or other simple systems. Usually they are "training" ANNs to match
databases which contain definite targets for what the output of the ANN should
be, for every single example in the database.
There are lots of uses for this kind of task. But that's not intelligence. That's not consciousness, that's not what the
mind does. We humans are not just simple
classification machines! This really ought to be obvious to anyone.
This situation is kind of scary; you have to ask what
is the relevance of that stuff? Now, I'm
not going to talk today about consciousness or the mind/body problem; if I'm
brave at SMC on
Monday I'll talk about
that[3,4,5], but here I'm going to focus on physiology.
If we agree that neuroengineering has been
caught in a kind of local minimum or intellectual rut, then what is the way to
get out of that local minimum? If you forgive a pun, I will argue that we can
get out of that local minimum by climbing out, by climbing up a ladder
-- and here's the ladder (Figure 2, on the next page), the ladder of designs of
neurocontrol.
Again, let me warn you that this is just a quick
overview; I'll be giving you citations to more detailed information later on.
There are many, many designs in this emerging area of neurocontrol,
which I define as the use
Figure
2. The Ladder of Designs in Neurocontrol
of well‑specified
neural nets -- either natural or artificial, just mathematically‑defined
neural nets -- to generate control outputs, which could be to motors,
muscles, glands, stock transactions or whatever, but real actions in the
real world.
In the neurocontrol field, we do have very simple
designs, and these are the most popular. They're easy to do; they're a great
start for people who want to get their students going, and start to build up
software. This is the right place to start, but these designs do have very
limited power, and they certainly are not like the brain.
In the middle level of the ladder, we have what I
call the state‑of‑the‑art group, and I'd say there are about
four groups that are really
in this category. It's curious that industry is here more than academia; I don't know why. Are university
people scared to do new things? I don't know, but these state‑of‑the‑art
groups have mostly taken a couple of years to build up; maybe that's the
problem, that you've got to keep your students around long enough, and build up
modular software packages. After a couple of years of struggling, these groups
have gotten real‑world applications just this year, of things that were
only on paper two or three years ago.
And they have proven -- with really exciting, important applications --
that these more advanced, more brain‑like methods are far more powerful
in solving real-world problems. There
are just incredibly important engineering problems that have been solved that
are in the mill; again, today I won't talk about this a lot today, but I may
make some reference to it.
After these methods on paper were used in real
applications, it was a challenge to us theorists to move ahead of the
applications people and come up with new methods to overcome the limits of the
older ones, so that now on paper this year there are new methods which did not
exist two or three years ago. And now,
on paper, it looks as if these designs and ideas really have the potential to
achieve true brain‑like intelligence. So my bottom line is that at least
on paper we now have the math we need to
understand real intelligence. I'm not
saying that these ideas are working yet on real systems, and that's what I try
to pay people to do, to climb up this ladder with real engineering systems.
By the way, I'm saying that the bottom level of the
ladder is a good place to start, but when I fund people, the higher they can go
up the ladder, the higher the probability of funding. They may have to climb one step at a time,
but they had better be moving upwards in a visible way. I'm trying to develop
the engineering math that will be necessary to understand the brain. I'm using engineering as a discipline
to get the math we need for what's really interesting, which is the mind and
the brain.
Four New Empirical Possibilities: A Summary
Now before getting into the
intricacies of neurocontrol, I would first like to give you my real bottom
line. I would like to summarize four empirical areas where I think new
experimental work could be really crucial. I will try to explain the reasoning
behind all this in more detail later, but for now I will just give a summary:
(1) First, I'm going to argue that some form of
backpropagation -- not the simple three‑layer kind that most people have
seen, but a more complicated, advanced form of backpropagation -- almost
certainly must exist in the brain in order to explain some of the capabilities
that we have observed there. That in turn suggests that we
have to look for some novel mechanisms, to carry information backwards both
within and between cells. Between cells, it is now well-known that nitric oxide
(NO) acts as a backwards transmitter. In addition, a group of researchers
including Timothy Bill -- one of the important pioneers in Long-Term
Potentiation (LTP) [6] -- has discovered a new presynaptic receptor intimately
related to LTP[7]. (The group speculates that this receptor may be involved in
adapting the nearby synapse, but there is no reason to believe that this is its
only function.) Back in 1974, after I had developed the backpropagation
algorithm, I speculated that the cytoskeleton might take care of the
backwards flows within cells [2]; this still appears to be a viable
possibility [5,8,9,10], but there is new evidence that the usual kinds of field
effects in membranes could also be involved[11]. David Gardner has shown that
such backwards mechanisms are crucial to learning even at the level of aplysia[12,13].
Nevertheless, all of this is only just a beginning.
There is a lot of engineering work needed in this
area, both in theory and in instrumentation.
It's really frightening to me, when I look at how critical the
cytoskeleton is in the nervous system (it is like half the nervous system!), to
see that the amount of work that's been done understanding how the cytoskeleton
relates computationally (or might relate) is negligible. We don't yet know that it's relevant,
but we don't yet know that it's irrelevant either. It is amazing to me
that we can just sit back and ignore it and give it maybe ten thousand a year,
when we're spending a billion dollars on the other half, when we don't know
what it does is. It's really
frightening; we really need to be studying the cytoskeleton in any case, and
backpropagation is just one of the things to look for when we do it.
In looking for backpropagation, you don't necessarily
have to look at the cytoskeletal level. There are other kinds of experiments
you can do, where region A has a forward fiber to region B (e.g., A might be a
part of the limbic zone and you move on to something like the motor cortex),
and sometimes you can find that the plasticity in A seems to depend on what
happens in B. It would be interesting to see if you could cut the fiber from A
to B and then see if you lose the plasticity in A. There's no way that could happen in a
classical neuron model that's all feedforward and membrane‑driven, but if
it does happen then that means that you can unhinge the neuron model. I
have tried to persuade Karl Pribram to look into experiments like that, and his
(informal, not for scientific publication) response was "I've already done
it, I've already proven this."
Pribram's response was really very interesting to me.
If you ask a lot of the middlemen between the neural network field and biology,
they'll tell you that this is impossible; however, when I ask Pribram he says
it's already been proven, that there is a backpropagation there. I don't know whether to take his informal
statements at face value yet; I think we need a lot closer collaboration to
evaluate those experiments to see what they mean mathematically, but it's clear
there is a lot to be done here.
(2) True reverse engineering
of hippocampal and other slices. In the talk by Sclabassi earlier today, we heard
some very exciting things about the hippocampus. It was particularly
fascinating to hear that the kind of learning you get from LTP clearly doesn't
represent the real nonlinearity of the system.
I would speculate that appropriate slices through the brain can generate
model systems that you can play with like artificial neural nets, where you can
control the inputs and outputs. Why is it that when we do experiments in neural
systems we try to always do them under natural conditions? If we think that biological neural circuits
are general purpose learning machines, then let's play with them!
Let's see if we can use a slice of neural tissue to
learn to recognize an
arbitrary pattern that
hasn't been seen in nature. Let's find
out what are the capabilities.
Let's find out what the plasticity is in these more micro, more
mathematical ways. And I would
speculate, for example, that a slice
through hippocampus and cerebral cortex that maintains those local recurrent
links will have a better learning capability, in a sense I hope to have time to
define, than any of the Hebbian
or backpropagation, feedforward nets that are in use today.
In other words, there are two classes of nets people
are using a lot -- the classic Hebbian, the Grossbergian nets, and then maybe
the multi‑layer perceptron (MLP) nets; I'm willing to bet that there are
critical learning problems which I hope to talk about, which that kind of slice
can solve better than any of the nets people now believe in, on the biological
or the engineering side. Once you prove this, empirically, then I have some
ideas for what is going on there, but the experiments are what's crucial for
now. I think if you do the experiment, you will shake up a lot of people, and
then they'll start thinking about those more powerful designs that we're just
now starting to look at in engineering.
There is a whole lot to be done in this area. Once
you have taken the first step -- demonstrating and describing plasticity on the
slice -- you can then start looking for the learning mechanisms that underlie
that plasticity. So in a way this might
be a good place to begin before getting into some of the harder issues I
discussed earlier.
Similar kinds of experiments could also be done in
culture, if the right kinds of cells can be grown together in culture. Many
biologists worry that cell cultures (and even slices) are very artificial. It
can be dangerous to draw too many conclusions from what we see in culture,
because the presence of other cell types and inputs in the brain could lead to
very different kinds of behavior. Nevertheless, when groups of cells in culture
do succeed in demonstrating certain kinds of engineering capabilities -
such as the ability to learn to approximate mathematical functions more complex
than those which Hebbian or MLP nets can learn -- then we probably can
conclude that these cells possess these capabilities (or more) in nature, in
the brain. There may be great value in figuring out what kinds of cells
need to be present, as part of a culture, to generate what kinds of learning
capabilities.
(3) A third area has to do
with the inferior olive, which governs learning in the cerebellar system. I am told by Pellionisz that Llinas and his
group have observed plasticity in the inferior olive, which is crucially
related to the cerebellum and lower‑level motor control. I haven't looked at the experiments myself,
but based on a very careful examination of the cerebellum, working jointly with
Pellionisz (not with tensor theory,
working with Pellionisz on some new ideas), it is my conclusion that something unusual is going on[14].
There are two possibilities ‑‑ or rather, I'm predicting one
of two possibilities. Both of them are very surprising. First of all, before
doing the experiment proper, the first stage is to replicate the phenomenon of
plasticity in the olive. Then you have to cut one of two fibers, and show that
cutting those fibers eliminates the plasticity; this would narrow down the
plasticity to one of two possible mechanisms. (The two fibers are: (1) the
climbing fibers; (2) the collateral fibers from the deep cerebellar nuclei and
vestibular nucleus to the olive.)
I hope that somebody can do this experiment soon. This
may well be the most finite and do‑able thing on this whole list
here. So I really hope somebody looks at
this. I have described that in more detail at the end of a recent paper[14].
This is an important experiment nobody has done‑‑I don't think it
should be that hard. And it is really
critical to our next step in understanding what the cerebellum is doing.
After this talk was given, I found out that the first
step -- of simply replicating plasticity in the olive -- itself a serious
challenge. The original experiments by Llinas et al, reported in Science in 1975, are still highly
controversial. Furthermore, there are certain learning tasks -- like those
described by Richard Thompson -- which do not seem to elicit plasticity in the
olive. (Just as most physical tasks only require the use of a few muscles, so
too do many learning tasks exercise only a part of our learning abilities.)
Hockberger and Alford at
A more technical issue, crucial to working out the
fine points of this system, is the ability of the cerebellum to learn time
sequences and delays [14]. This ability clearly depends on certain
short-term memory capabilities of Purkinje cells, but it is very tricky to
design a circuit which reproduces such capabilities. (See chapter 13 of [15].)
Tam, at the
(4) Fourth, there is room
for more true reverse engineering of the cerebellar motor system. Suzuki, Kawato et al[17]
have done a magnificent job in getting this area started, but a lot more needs
to be done. Suzuki et al have basically shown that the lower motor system is
doing optimal control, not adaptive control in the classic sense, and not
translation between different kinds of coordinate systems, but optimal
control. I think that someone could play
with that circuit a lot more than anyone has done so far. Suzuki et al, and Houk,
think they know where the reward or utility functions are coming in from; if
they are right, we could perturb these inputs and prove what the power is of
this system in optimization, in adapting to new regimes. Again, we could
play with the lower motor system, by perturbing its inputs to see what
capabilities it has as a general‑purpose optimizer.
In brief, I have described four general areas where
new kinds of experiments could be extremely useful. I don't know if I'm
describing the tasks in exactly the right way. This is just an attempt to get
the process started. I'm just a dumb engineer, as they often say. But I think that something needs to be done to get us moving into these
new kinds of areas, and there is some theory behind the ideas above.
SUPERVISED
LEARNING: RECENT ANN RESULTS
AND
IMPLICATIONS FOR NEUROCONTROL AND BIOLOGY
Supervised Learning As A Neural Net Paradigm
A lot of people in
neuroengineering get upset when I talk about control applications and control,
because a lot of people in the artificial field really have this old idea
(illustrated in Figure 3), that supervised learning is the same as neural
network theory. They think that neural
network theory is the same as learning a map from an input vector X to a target vector Y, in hopes that in the future
you'll be able to predict the right target vector. And you go through training sets and you
learn over and over again what this mapping is.

Figure
3. What Does Supervised Learning Do?
In fact, if you look at the Granger‑Lynch model
of the hippocampus (arguably the best existing model of the hippocampus as an
associative memory) ‑‑ that's another form of supervised learning;
it's just plain old pattern classification you're studying. Supervised learning tends to be an
all-pervasive paradigm, even for biologically motivated research. Many people
tend to think that supervised learning is fundamental theory, and that anything
else is just dirty applications.
Supervised Learning versus Neurocontrol
Supervised learning is
certainly useful, and it may well exist in subsystems of the brain, but
it turns out that for really powerful control systems, you have to do stuff
that is a lot harder.
What you have to do is stuff like this (see Figure 4
on the next page). When I'm giving a tutorial on how to do real neurocontrol in
engineering, it turns out that I have to spend an hour or two on each one
of the three main boxes in Figure 4. You
do have supervised learning systems in these designs, but they're like little
modules. And then you have a big system,
a neurocontrol system, that takes these lower level modules and integrates them
and links them. I often compare this
situation to how we build computers: there's a lot of science to building the
chip, but there's a lot of science to putting chips together to making a
computer. Supervised learning is a general purpose concept, but neurocontrol is
also general-purpose and fundamental; they simply address different
general-purpose tasks.
It turns out that the work that's been done in
neurocontrol at these multiple levels of organization has parallels to the
brain, at multiple levels of organization.
So the stuff we've learned down at the supervised learning level tends
to be relevant to issues like what is the circuitry like within the cortex,
within recurrent nets, or within the cerebellum, while the
higher-level stuff is important when we try to figure out the organization that
connects those systems. So that
means I should talk about both of these levels and explain them before I
talk about the brain. So I should spend eight hours before it all becomes
crystal clear. Forgive me, it won't be
quite as crystal clear as I like, because I don't have the eight hours.
Figure
4. Four Task Areas Critical to Neurocontrol
Three Supervised Learning Modules Used Today in Neurocontrol
First of all let me talk at the low level,
at the supervised learning level. Little
nets that learn pattern recognition. What has been useful in engineering?
Basically, there are three kinds of
networks that people really use in real‑world control
applications:
(1) The most common is the
multilayer perceptron (MLP). (See Figure 5 on the next page.))
Please don't call it a "backpropagation network"! The MLP is only one special case of what you
can adapt with backpropagation. Furthermore, the MLP is a lot older than what I
did in 1974. Bernie Widrow or Rosenblatt are the guys that should take credit
for the MLP design itself.
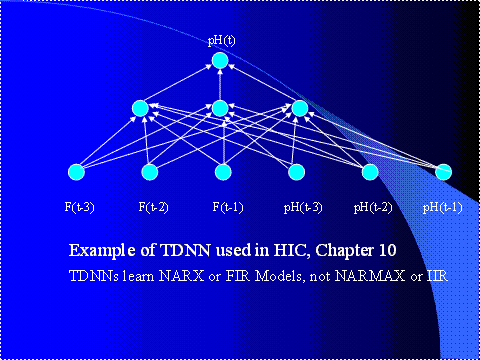
Figure 5. An Example
of a Three-Layer Multilayer Perceptron (MLP)
The MLPs are basically the McCulloch‑Pitts
networks, the feedforward things. There have been some wonderful theorems about
what they can do.
(2) and (3) Almost as common
are the CMAC and the RBF designs. (Figure 6) These networks are examples of
"local" learning systems. We have already heard about these designs
from Nick DeClaris; for example, CMAC was first proposed by Albus, for a PhD
thesis under DeClaris. There are many other local learning systems discussed in
neural net meetings, but DeClaris' students happened to hit on what was useful
more than most students. There are also many modified versions of the CMAC and
the RBF, which give improved performance in control applications[15].
Figure
6. Structure of CMAC or RBF Network
Basically, these local learning rules perform
forecasting by association. The MLP
gives you a global model and is good for learning global functions, causal
relations, etc. The local systems are
more like forecasting by
precedent. When you've got a new situation, you predict the result will be like
what it was before when you had a similar situation. It's an associative memory, and
this is what the Granger‑Lynch
stuff is, just another example of the same general principle.
So these are the things that most people use. These
are feedforward nets, easy to implement and I'll show in a couple of charts how
some people have used them. There are many other forms of associative memory,
based on Hebbian learning, which have appeared in the biologically oriented
literature; however, those kinds of nets are not used very often, for one reason
or another. Most likely, people feel that the Hebbian nets now available are
very similar in capability to the CMAC and RBF, because they are based on
forecasting by precedent, while being harder to implement in real time. Why
work harder to achieve the same capability? Another factor, however, is that
people do tend to implement what is easiest first, not what is most powerful.
Local learning systems can be adapted in a variety of
ways -- through least squares, through backpropagation (i.e. derivative-based
learning), etc. No matter how they are adapted, they tend to be faster to adapt
than global MLPs, because they do not have to "undo" what was learned
in a previous region of space when they explore a new region of space. They are
usually set up so that different weights are active in different
regions of space. They tend to require many more weights, but learn faster.
There may be ways to combine the best advantages of global and local networks
together in one system[18], but no one has implemented the right kind of hybrid
as yet.
What Kinds of Functions Can Such Modules Represent?
So what are the capabilities
of these different kind of networks? Well, there are a lot of theorems. There's a guy named Andy Barron who has
proven some beautiful theorems showing that those three‑layer neural nets
like MLPs are much better than
In control applications, however, to really control
an arm efficiently, sometimes you don't have a smooth function. Then you've got a problem and it often
doesn't work, and a lot of control applications three layers won't work. So, a guy named Sontag at
But there's another problem. You can approximate any
function, but you need to approximate it parsimoniously. MLPs are as good as any other feedforward
net, but in general there are some functions which you cannot approximate
parsimoniously with any feedforward net. This means that you need
enormous numbers of hidden layers to approximate them, and enormous numbers of
hidden neurons.
Marvin Minsky, years ago, gave an example of this in
his famous book Perceptrons. He described the "connectedness"
problem, which sounds at first like a very typical character‑recognition,
pixel‑type problems, but it turns out to be a little different. Imagine
that you've got a grid of 50x50 input pixels and that they're all either white
or black, and that you're trying to recognize a desired pattern. What you're trying to do is to output a one
if the blacks are all connected, and a zero if they're not.
Now it turns out that Minsky showed that the number
of hidden units required for this task is just enormous. As the number of
pixels grows, it becomes astronomical; no feedforward net of any kind is going
to do a good job. But if you allow
recurrence, recurrent feedback connections, what I call simultaneous recurrence
(a special kind of feedback connection), then you can represent
it parsimoniously.
I would argue that the kind of language-processing
problem that Jim Anderson described earlier (from Fodor) is a problem in this
family, where a feedforward net can't represent it parsimoniously, but a
simultaneous recurrent net can represent it parsimoniously. And I've seen systems of that general sort,
which so seem to work on that kind of problem, but I haven't studied Fodor's
example in great detail.
It turns out that, if you want to deal with control
problems like navigating a robot through a cluttered room where the clutter
keeps moving and it's in a new position, you need to worry about finding a
connected path. So there are good
arguments[15,18] that higher‑level intelligence has to use these kind of
networks.
So that seems easy, but is it? Well, first of all, what happens if you have
parts of the brain that have to make decisions quickly? Simultaneous-recurrent
nets take time to settle down‑‑what then? Then you've got to have a feedforward net,
and what happens then?
Fast Feedforward Nets: The Cerebellum
Well, Figure 7 (on the next page) shows an
example of a feedforward net with two hidden layers that is good for fast,
general motor control. This comes from
Nauta[1]; it is a diagram of the cerebellum. In the cerebellum, you start out
with inputs along the mossy fibers (which some people would call an input
"layer"). These inputs go to the granule cells, which operate as a
first hidden layer, and you've got zillions of them. Some people say there are
more granule cells than there are any other kind of cell in the brain, maybe
ten times that number. That reinforces
the point‑‑you
need a lot of hidden nodes if you try to do complex tasks with a (relatively
local) feedforward net.
The next hidden layer in the cerebellum is
the Purkinje cell layer. The output layer is basically the deep cerebellar
layer and the vestibular nucleus (the FTN cells of the vestibular nucleus, to
be precise); those two systems are basically together ‑‑ they're
not right next to each other but they form one output layer, for functional
purposes. In summary, the cerebellum is not based on simultaneous-recurrence,
which is slow but powerful. Strictly speaking, however, it is not just a static
MLP, either. Above all, the Purkinje layer has some working memory
capabilities[14], similar to well-known ANN designs. Such capabilities are
tricky to adapt[15, chapter 13]; this, in turn, suggests that Purkinje cells
might possibly be adapted by a combination of the well known
olive-to-cerebellum mechanism, plus a local mechanism supporting the
working memory effects. Also, because the Purkinje cells are large cells, and
because continuity in output is very desirable at this level, it is conceivable
that dendritic field effects, as described by Pribram, could occur within these
cells[4,18].
Figure
7. The cerebellum, from Nauta [1]
Slower, More Powerful Nets: The Cerebrum
But again, this kind of
feedforward arrangement is not very good for the really higher‑level
kinds of functions like finding a connected path or connectedness. There are
some kinds of functions you just can't expect the cerebellum to solve, because
they require a more sophisticated processing.
That leads to a prediction that somehow or other the higher levels, like
the limbic lobes and the cerebral cortex, must form a kind of two‑level
system, where the low level is settling down...but first let me describe Figure
8, which shows what a simultaneous recurrent net (SRN) is.
Figure
8. A Simultaneous Recurrent Network
Mathematically, an engineer would say that you plug
in the inputs into any old feedforward structure (the net labelled f in Figure 8). But then you
take the outputs of f, and
feed them back in as inputs to f,
and see how that changes the outputs. You keep feeding the outputs back in as
inputs, again and again, until the values of the outputs settle down to some
kind of equilibrium, y∞.
Now, to use a system like that... you have to plug in the inputs, wait through
many cycles of the inner system f
until the outputs settle down, and then that becomes just one cycle time
of your bigger system. Now, when I first
saw the engineering of this[15], I said this can't have anything to do with the
brain, because you need really fast cycles inside of a longer cycle; how could
that be biologically plausible? I knew
that we needed all this to get intelligence in engineering, and I couldn't
think of anything else; therefore, in the 1990 Decade of the Brain Symposium
(sponsored by the National Federation for Brain Research and the INNS), I
presented this from an Engineering point of view, without any notion of how the
connection to the brain could be made.
Later that same day, Walter Freeman presented his
model of the hippocampus, which involved exactly the same kind of loops
within loops as in my model! He showed how very close inner recurrent loops
operate at a very high cycle time, embedded within a larger, slower theta
rhythm. For the inner loop, he said that the basic calculation cycle time is
like 400 hertz, versus about 4 hertz -- quite enough to implement Figure 8.
(Some people quote 80 hertz -- based on Fourier analysis rather than cycle
times -- but that still would be enough for some functionality in this design.
When I checked with Pribram, he assured me that fast, 1ms. synapses allow such
high-frequency computation.) VonderMalsburg has convinced me that such
dual-loop effects are even more certain to occur in the neocortex, but the
neocortex contains additional capabilities and complexity which may make it harder
to work with at present. I would speculate that SRN capabilities are crucial
both to binocular vision and to the image segmentation capabilities of
neocortex.
In brief, the biological data appears to fit the
model beautifully. Now, if you look
at Granger and Lynch's model
of the hippocampus, it doesn't do that.
In their model its like a feed forward, associative memory, and you only
have an outer recurrence that's used to generate the
associative memory. So what is that inner loop doing? Maybe the hippocampus is more powerful than
associative memory. Maybe we need something more powerful than an associative
memory to form emotions and make plans in our life, and maybe somebody can do
an experiment proving it. I hope
so.
Parenthetically, it should be noted that SRNs --
unlike feedforward networks -- can have problems in settling down to a stable
equilibrium. In engineering, one can use a "tension" term [15,18] to
reduce the probability of instability, but the possibility cannot be totally
eliminated. The tension parameter is a global parameter, with an interesting
analogy to the global level of adrenalin in the bloodstream. Karl Pribram has
pointed out that there is a strong analogy between this "tension"
term and the "unpleasure" principle of Freud[19], which plays a key
role in understanding the possibility of instability in human brains. In the
human limbic system, Pribram's empirical discussion [20] suggests that the
hippocampus is an SRN, acting mainly as a "hidden layer" of the
limbic network, a network in which the amygdala is the ultimate or penultimate
output layer. (This suggests a kind of crude analogy between the hippocampus
and the cerebellar cortex.)
Other Forms of Hebbian Learning
That covers most of what I
really want to say about supervised learning. Again, please excuse my glossing
over the many, many details; each one of these topics can be discussed in much
more detail, and is so discussed in the papers cited.
For the sake of completeness, however, I should say a
little about two forms of Hebbian learning which I did not mention
above.
Most people who work with Hebbian learning would
argue that there are really two different kinds of Hebbian learning system
which could be used on supervised learning problems. There are local
associative memory systems, which I discussed above. But there are also global
systems, which are generally linear, and require that inputs be decorrelated
before they enter the supervised learning system. A lot of decorrelating
networks have been designed for use with such nets. However, after discussing
this matter with Pribram, I am convinced that this latter class of network is
not relevant to systems like the human brain. Pribram and others have shown
again and again that biological representation systems have a great deal of
redundancy (e.g., like wavelets but with a 1.5 amplification factor instead of
2, etc., as in the Simmons talk today). One would expect such
redundancy, in any system which also has to have a high degree of fault
tolerance. This is inconsistent with the mathematical requirement of
orthogonality. In addition, the limitation to the linear case is not
encouraging, either.
In 1992, I developed an alternative
learning design which appears Hebbian in character, but has radically different
properties[4,18]. It provides a mathematical representation of certain ideas by
Pribram about dendritic field processing, which the talk today by Simmons
provides strong empirical support for. It is closely linked to Chris Atkeson's
experiments with locally-weighted regression, which has performed very well in
robotics experiments at MIT. In retrospect, as I reconsider the issue of
information flows around dendrites, I suspect that the design still needs to be
revised, to account explicitly for the three-dimensional nature of local
information flows, at least for biological modeling. In any case, the
alternative design is still feedforward in terms of what it accomplishes;
therefore, it might possibly be worth considering as a model of the innermost loop
of the neocortex, but it does not obviate the need for simultaneous recurrence,
and for the unusual kinds of nonHebbian feedback (as in Figure 8) required to
adapt key parts of the neocortex and hippocampus -- if those systems are as
powerful as I suspect.
Summary
In summary, I predict that
the human brain contains some very complex circuitry, as required to solve some
very complex adaptation problems. At present, most people would find it hard to
believe that something that complicated is there, even though it does fit these
new results of Freeman and so on. I think we need new experiments, based on
living slices, to help get home to people that it's this kind of complexity
that's in that system, and that the old models are simply not good enough. So that's the end of supervised
learning.
THE
HIGHER LEVEL OF ORGANIZATION: NEUROCONTROL
Now let me talk about
neurocontrol. This is a subject I've
talked about for eight hours at a stretch, so I will have to cut out a lot of
important material here today. First, I want to talk about why this is crucial
to understanding intelligence. I'll skip over my slides on engineering
application areas. I will talk a little bit about the kind of designs
that engineers are using today, but only a little. Mainly I will focus on the design concepts
which relate directly to understanding the brain.
Why is Neurocontrol the Right Mathematics For Understanding the Brain?
This is a chart (Figure 9)
that people look at and say, "I already know this." But if people could understand the
implications of what they already know, this world would be a different place.
There are some implications in what we already know that people haven't thought
through. Now what I am going to talk about
here is the reason why the human brain is a neurocontroller; let me give you
the argument in a few stages.
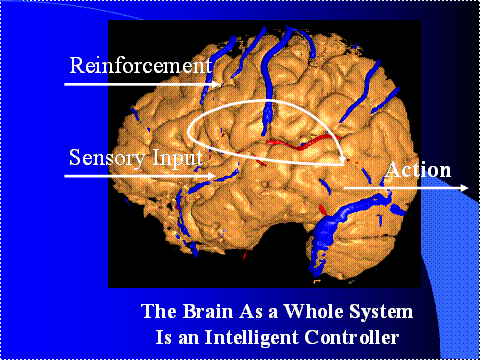
Figure
9. The Brain As a Neurocontroller
Step one: we know that the brain is an information
processing system. I would call it a
computer, except that people will think of sequential machines. But it's really a computer; it's an
information processing system; its sole biological function is to be a
computer. And what does it compute? It computes actions that control
glands and muscles. So the point is that
the function of the brain as a whole system is to perform control.
Some people think of control as something that's only
in the cerebellum, just to control finger movements. That's not true. Nauta, in his classic text on
neuroanatomy[1], stresses how you cannot separate what is the control system
from the rest of the brain. Now that
doesn't mean that the whole brain does tracking or pursuit movements; no, it
doesn't do that; it does a higher order kind of control, of course. And you might use the term "sensorimotor
control," if you will. But the
point is that the brain as a whole system has the function of
calculating these things. Everything in
the brain is there to help it compute these outputs. So the function of the brain is to do that;
if you want to understand the brain as a whole system, you have to understand
the mathematics of what it takes to build a controller that has these kind of
control capabilities, which again go far beyond mere trajectory tracking.
(Those who think of control as trajectory planning may still have
troubles with this; I urge them to reconsider the definition of control,
and recognize that the overall mathematical literature on control has always
been far wider than this in scope.)
Furthermore, you can't even understand a subsystem
until you know how it fits into the whole system. Therefore, you can't even
understand subsystems of the brain until you put them into this greater
context, which is neurocontrol: the brain is a neurocontroller.
Capabilities of the Brain As a Controller
So, next slide (Figure
10). This slide shows what I regard as
the most exciting and crucial capabilities of the brain as an intelligent
controller. I should have added an extra
line here about learning in real time; it's just so obvious, but it's something
we've got to keep in mind.
Figure 10.
Capabilities of the Brain As a Neurocontroller
The brain can control millions of actuators in
parallel -- well, maybe only 900,000 ‑‑ it's the same principle,
huge numbers. What about conventional controllers? Most control engineers
regard one actuator as a normal problem and ten as a large problem. Thus the brain has an incredible capability,
very exciting to engineers. It can
handle nonlinearity and noise routinely, without being destabilized. And above all, most critical, it includes
what you might call a long‑term planning horizon. The AI people would say the long-term
planning capability is the real intelligence.
And the brain also has a high‑speed coordination capability
through the cerebellum, basically.
Brain Capabilities Versus ANN Capabilities
Now, how do these
capabilities compare with anything we can conceive of in mathematics? Is there any hope of understanding them? Well, we presume there's a hope of understanding
them, but is there a way that we can conceive of to understand them?
The next slide (Figure 11) provides a list of what's
been done in Artificial Neural Networks in control. These are the basic kinds
of capabilities that exist today. I've
read hundreds of papers on this topic, but they all boil down to this. I've seen a lot of people try to wriggle out
of my basic taxonomies, but these are basically the capabilities you've
got. You've got people using neural nets
in subsystems in control; that's not really neurocontrol. You've got people who have learned to clone
experts, learned to copy a human movement.
You've got people who
NEURAL NETWORKS (ANNs)
IN CONTROL:
1. In
Subsystems
2. Copy
Experts
Supervised
Control
3. Follow
Path, Setpoint, Ref. Model
Direct
Inverse Control
Neural
Adaptive Control
4. Optimal
Control Over Time
Backpropagation
of Utility (Direct)
Adaptive
Critics
Figure
11. Four Tasks Performed by ANN Controllers
(Subsystem,
Cloning, Tracking, Optimization)
do classical adaptive
control, which is just a matter of trajectory tracking; for example, somebody
tells you where to move your arm and you move it there. And then you've got
systems that optimize over time.
Now, cloning or copying is definitely not what humans
do. I admit that we may imitate our
parents a little bit, but
they don't tell us exactly what to do; they don't give us a complete vector of
actions, and that's what the cloning designs require.
Likewise, we're not simple trajectory followers. We
don't have somebody who tells us where to move our arm; maybe we have
subsystems -- maybe, maybe not -- but that isn't what the human brain as a
whole does.
So, that really leaves us only one choice, which has
to do with optimization over time. Now,
the notion of optimization over time is one people have taken seriously for
centuries in studying human behavior. People have screamed at the idea for
centuries as well, because it's clear that humans don't do a perfect job of
optimization, but that's okay. If, in
engineering, you do the best possible job of optimization, your system still
won't be perfect. You don't have to worry about designing a system so perfect
that it's implausible as a model of the human brain; in fact, that's the last
thing you have to worry about, okay?
There are a lot of imperfections in the engineering optimization systems
quite close to those you see in biological systems.
Furthermore, the general concept of reinforcement
learning is very pervasive in animal behavior. There's a guy named Harry Klopf
who has recently shown that if you take some very simple optimization networks,
they regenerate not only what's called Skinnerian conditioning (in other words,
conditioning by reward and punishment); just incidentally, they replicate
Pavlovian conditioning as well. So this concept really is powerful enough to
cover the basic things we observe.
In summary, my argument here is that the optimizing
designs are the only form of neural
networks we know of, the only form of mathematics we can conceive of,
which is really relevant to understanding brain-like intelligence. It seems to
me that it's got to be what's going on in the brain.
If you look again at Figure 11, you will see that
there are only two useful ways of doing the optimization over time (for
large-scale problems). There is a thing
called backpropagation of utility: I proposed this approach in my Ph.D. thesis
in 1974; I invented it, so I have a vested
interest in it, but I'll still tell you it's not biological. Flat out, it's not biological. I can explain why at length, if anybody's
interested. I've written it up[2,15]; it's not biological. There's only one thing that's biological, and
that's what I call adaptive critics, and I'm going to say that the brain is an
adaptive critic system. I've got to
explain what that means now.
ANN Control Designs Versus Brain Capabilities
Table 1 is a matrix
comparing these designs against the capabilities of the brain. For the most
part, this table simply reinforces what I just said, that the simple cloning
stuff doesn't involve planning, that tracking
Table 1. Matrix
of ANN Designs Versus Key Brain Capabilities
trajectories doesn't involve
planning either, and that backpropagating utility is not brain‑like
because it can't handle noise and it's not so good for real time. But if you
look at the table, you can see that it subdivides the world of adaptive critics
a little further.
There was an old class of adaptive critics developed
by Barto, Sutton and Anderson in 1983. It was a very useful first step in
popularizing the idea. It can handle noise and optimization
over time and real time
learning. A lot of people are having fun with it. It's good for a lot of
engineering applications, but it won't handle many motors. And people have to understand it's very
limited; it can't handle large problems.
And when I say large, I mean like ten variables in an aircraft control
problem. I mean that this is a really
heavy limitation and that's been proven empirically now. (Tesauro has shown
that a challenging AI problem -- playing backgammon -- yields very well to this
design; that problem involves many theoretically possible states, but still
involves a limited number of discrete action choices. Haykin's new book reviews
the engineering experience -- which fits my summary here -- and White and
Sofge, among others, have reported similar experience[15].)
On paper, in 1987 (actually before '87, in 1977), I
proposed an alternative class of adaptive critics which combine backpropagation
with adaptive critics. And let's call
that Advanced Adaptive Critics. Combining backpropagation with adaptive critics
in a fundamental way, not in a superficial way. And on paper, it looked to me
that this approach solved the problem of handling many variables at once. And, as I said, I published that in 1977 as a
solution to the slow convergence problem of the simpler critics. So that was actually before the Barto‑Sutton-Anderson
paper on the same kind of area.
In 1987 there were no working examples, but some
people heard me present this in mid‑1989 and now there are four working
examples, at least, and two that are pretty close to real, and two of the examples are in large uses. There is one company that is a spinoff from
McDonnell‑Douglas (Neurodyne[15]) that has used these things to solve
composite materials manufacturing problems that could never be solved before by
any kind of neural network method, where the two nets would not work because
they couldn't learn fast enough in real time. They have also used it in the
control of an F‑15 (providing real-time adaptation to aircraft damage in
two seconds), to the control of a prototype of critical systems in the National
Aerospace Plane, and elsewhere.
So there are actually many
applications in one of these groups. (See [19] for some further applications.)
So the bottom line is this: we now have real‑world
examples of advanced adaptive critics, and they have indeed proven much more
powerful. But we have other designs that
nobody's tried yet, that are on the books, and we're just waiting to go up the
ladder another step or two. So there has
been proof that this kind of design works.
Where to Get Mathematical/Implementation Details on Neurocontrol
Designs
There is no time today to
describe all the ins-and-outs of the different adaptive critic designs, let
alone all the other designs which have proven useful in some engineering
applications. Today I will mainly focus on a few points about adaptive critics which
I think are biologically relevant. But I
can give you some citations that tell you how to implement these designs.
In this field, it is really critical to get the right
citations. Frankly, there are a lot of
papers and books out on neurocontrol or on recurrent networks which are wrong
or obsolete; there are a lot more than you might expect. I have seen a lot of
very bright people having a very hard time adapting recurrent networks, for
example, based on believing some things they read by world-famous people, who
should have known better. So I really want to stress these citations.
Until December of last year (1991) I spent at least a
good year working with people in industry and academia, and on my own, to come
up with a complete statement of where we are in terms of the state‑of‑the‑art
designs and the new ideas. The results are in a new book called the Handbook of Intelligent Control, which
finally came out in September 1992[15]. This book is the up‑to‑date,
complete source on what is known in neurocontrol today. It contains an authoritative statement not
only of my own views, but of many other key workers in field, along with truly
real-world benchmark problems and applications. (See [19] for further
applications and information on patents.)
Now, there is still a problem here. Because this book
is a complete handbook, it is not an elementary textbook. In order to get a
basic introduction that goes a bit beyond what I am saying here today, there
are two conceptual overviews I would recommend: [22], and [19] or [23]. If you're a good enough engineer, the Handbook
might even be straightforward enough by itself, but if you find it a little
hard going, these introductions may be important.
I have a friend who's begun to implement some of the
very hard architectures in the Handbook, and he says that it's been very useful
for him to refer to the tutorial in [22].
He says that [22] is the easiest‑to‑read thing that I have
ever written, and he says that this tutorial is very, very important in really
implementing neurocontrol in a hardcore engineering way.
So reference [22] is for mathematical details; the
other references -- [19] or [23] -- are for
conceptual details, and
applications, and excitement, and that kind of stuff. They are good for policy
people. You need [22] only if you really want to implement neurocontrol and
understand the math in detail. Reference
[23] has the advantage of being shorter than [19], and being more easily
available; reference [19] has the advantage of containing new information about
how to combine neural nets and fuzzy logic, as well as some basic background on
ANNs.
Neurocontrol Designs to be Discussed
Now, aside from these
references, I am not going to talk at all about those forms of neurocontrol
which are relevant only to engineering. I won't talk about cloning. There are
neat applications of cloning in controlling a model of the National Aerospace Plane,
but I won't talk about them today. I won't talk about neural adaptive control,
even though it's painful, because those designs do raise some issues of some
relevance to biology. Within the realm of optimization, I will not talk about
direct methods like the backpropagation of utility, even though there are
important applications like improving efficiency and reducing pollution in
chemical plants[15]. I will talk briefly about direct inverse control --
an approach to solving tracking problems, because some people believe that
approach is relevant to low-level motor control in biological organisms. Then I
will talk about adaptive critics -- a more relevant family of designs -- in
more detail.
Direct Inverse Control (A Simple Approach to Trajectory Following)
Direct inverse control I've
got to talk about because there are a lot of people who tacitly assume that
this is what the brain does.
I was really glad to hear Dave Robinson talk at this
workshop about how people think the brain is mapping from coordinate system A
to coordinate system B, and about why this is a fundamentally misleading
assumption. I agree with Dave very strongly that that is a bad way to describe
what goes on in the cerebellum. And
why?
People assume that the cerebellum is doing something
like this (Figure 12). Suppose that you're trying to get a robot arm to follow
a trajectory in physical space. You've got spatial coordinates X1 and X2. You
control the
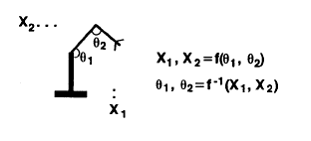
Figure 12. Direct Inverse
Control
thetas (joint angles).
Somebody else is going to give you the X's, and you've got to figure out what
are the thetas that get you to the right X's.
Physically, you know that the position (X1,X2) is a function of the
thetas. So if this function is
invertible, then the thetas are a function of the X's, and what you can do is
this: you can flail the arm around, get data on the thetas and the X's, real
data, and then learn the mapping from the 's to the thetas. That's the basic idea. People like
Kuperstein have taken this kind of approach, and people like Miller have done
it, too. Kuperstein was an important pioneer in getting this approach started,
but his reported error statistics (circa 3 percent) were too high to be useful
in a practical way in robotics. Even in biology, we know that more accurate
tracking is accomplished. I am puzzled why some people in neural nets go back
so often to that early work, now that Kuperstein himself has moved on to other
problems.
Now, Miller has shown that you can fix up the basic
error statistics[15,17], but we still know that the human arm has many degrees
of freedom. We know there are a lot of degrees
of freedom in the human arm, more than
there are in space; thus we
know this mapping is not invertible for the human arm. So what is going on
here?
Suzuki, Kawato and Uno have done a lot to
explain this situation. They have lots of experiments proving that there is
actually an optimization going on in this motor control system of the
human arm. The details of that are in many places; for example, we have an MIT
press book[17] where Kawato talks about that, and their experiments are
unbelievable. I know that Hogan from MIT
has recently questioned their
conclusions, but neutral observers like Massone at Northwestern have looked
over this controversy; it is my understanding that the empirical evidence is
overwhelming that Suzuki et
al are right on this particular point.
So we have a real optimizer down there in the
cerebellum; we don't have the direct inverse coordinate-mapping kind of stuff;
and that leads to some very interesting possibilities. Somebody should do some
experiments to see how flexible and plastic that system is as an
optimizer. Can they change what it
optimizes? Can they use it to solve interesting optimization problems? And then the question is: how does it do it
biologically? How does the cerebellum
act as an optimizer?
By the way, there are a lot of engineering
applications of direct inverse control. For example, it has been used to
control a simulator of the space shuttle main arm; you may be seeing the
results on television in a few years, if all works as expected, but I don't
have time to get into those kinds of details today. The bottom line is that
direct inverse control has its uses, but is not relevant to the adaptive part
of the human brain.
Adaptive Critics:
Now let's talk about
adaptive critics.
One way of defining adaptive critics is to call them
systems to approximate dynamic programming.
When I give this definition to engineers, they say, "Oh, you're
talking about something real. I thought it was garbage. You mentioned Freud and
animal learning, so I assumed this can't work." But actually, you know that animal learning
really does work; it is a powerful information processing system. Still, it is
legitimate to look at it as an approximation to dynamic programming; that is one legitimate point of
view.
In engineering, it is well‑known that (for good
mathematical reasons) there is only one set of techniques that is capable of
finding the optimal strategy of action in a general, noisy nonlinear
environment over time. There's only one
that can do that in a general case, and that's called dynamic programming.
Figure 13 illustrates the basic idea of dynamic
programming.
The way that dynamic programming works is that you
give the system a utility function U or a performance function or primary
reinforcement ‑‑ there are a thousand names for it; in other words,
you tell it what you want to optimize over time, over the future. You also give it a stochastic model of the
environment. Then, what dynamic programming does is that it comes out with
something called the J function -- at least that's what Bryson and Ho
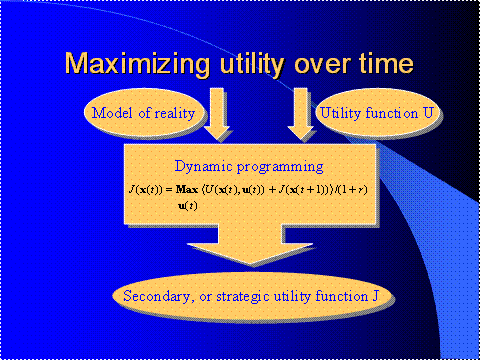
Figure 13.
Inputs and Outputs of Dynamic Programming
call it. (To be more
precise, in dynamic programming you solve an equation called the Bellman
equation, in order to find this function J.) I like to call this function J a
"strategic utility" function. It's just another utility function; it
looks similar to U, in many ways.
The basic theorem of dynamic programming is this: if
you maximize J in the short term, that will give you the strategy that
optimizes U in the long term. So dynamic
programming translates a difficult
problem in planning or optimization over time into a problem in short term
optimization. That is the essence of
it.
And then the next question is: if there is only one
exact way to do this, why don't we use dynamic programming for everything? In engineering and in biology, why don't we
use it for everything, if it's the only exact and perfect thing? Well the reason is simple: it's too
expensive. It may be the minimum-cost
method, but the minimum cost is astronomical even when you have just a few
variables. You can't do it exactly. A corollary
of that is nobody will ever come up with a neural network that plays a perfect
game of chess. So the next time a
computer scientist tells you "gee, perfectly adapting a neural net is an
NP‑hard problem; therefore this isn't real and
we've got to give up on
it," ignore the computer scientist.
The goal is not to play a perfect game of chess; that isn't what the
brain does; and that isn't what our artificial systems can do, because it can't
be done. That's one reason why the
systems aren't perfectly optimal: it's not possible in a real‑ world
engineering sense.
So what can you do? For a real‑world, general purpose
system that tries to optimize in the real world, we have to come up with a general
purpose approximation to dynamic programming. That's what adaptive critics
are. More precisely, adaptive critic
systems are systems which contain networks whose job is to approximate either
the J function of dynamic programming or its derivatives or something very
close to it. That's what it is; you can
call this "approximate dynamic programming" if you've got to sell it
to a boss that doesn't like neural nets, and you'll be completely honest. You can call it adaptive critics among neural
network people, or -- if you're talking to animal psychologists -- you can call it reinforcement learning,
although that tends to understate what it's good for. Those are all legitimate
names for what I am talking about here.
Intuitive Meaning of U and J
Now let me give you a little
intuition about the meaning of all this, because once again, I'm saying the
human brain is an adaptive critic system.
So I am claiming we have a network in our brain that approximates the J
function. Table 2 gives us some intuition of what the J function
is. If you're playing chess, the
ultimate goal, at least in computer chess, is to win and not to lose. That's the intrinsic utility, U. But there's a famous rule of thumb, that a
queen is worth nine points, a rook is worth five, etc.; people use that rule of
thumb to see if they are making progress in the game. Beginners play to
maximize points. Sophisticated people
learn that holding the center is also worth something. And there are studies of Bobby-Fischer type people which argue that
Table
2. Examples of U and J

they don't really see ahead
twenty moves -- even though they love to talk that way ‑‑ but that
what they really do is to perform a very complex recurrent, strategic
assessment to understand how well they're doing. And they really look ahead one move, but they
do a complicated, strategic assessment of their options one move ahead.
In humanistic psychology you could think in terms of
pleasure and pain, and hope and fear. In typical animal psychology, there's
primary reinforcement and secondary reinforcement. This U/J concept occurs all
over. I don't think this concept is new
to me; it's been hard‑wired into our brains for years. But maybe we're just making it mathematical
for the first time.
So when I say that the human brain is an adaptive
critic, what does this theory really mean? In common-sense terms, all I'm
saying is that we're governed by our hopes and fears, and these phenomena of
hope and fear are irreducible things built into the human brain. I think that
this is plausible. I don't think that it's a weird AI kind of theory, that
hopes and fears are the fundamental grammar or representation wired into a big
part of our intelligence.
The Barto/Sutton/Anderson Design
Figure 14 illustrates the
2-Net design I mentioned earlier. Because I don't have much time left today,
let me explain very briefly the main reason why this design can be slow. The
problem is that you've just one global reinforcement
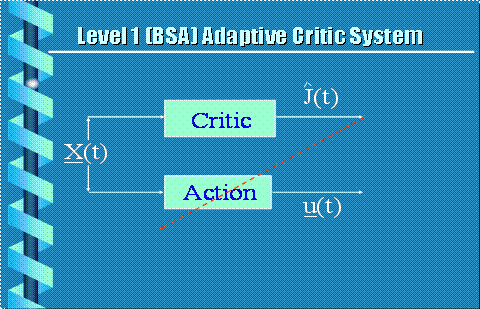
Figure 14. 2-Net
Adaptive Critic of Barto, Sutton and Anderson
signal broadcasting to an
action net. If you only have one action,
then you know which action was wrong.
But if
you've got a hundred
actions, and you made a mistake, then you don't know which one to change, in
what direction. You don't have a sense
of cause and effect; without cause and effect, it's kind of hard to learn. The ideas
in this design may still be useful as part of a larger hybrid, but, by
itself, this design could never describe a large-scale system like the
brain. So now let's move on a little
bit.
The Backpropagated Adaptive Critic: From Freud to Engineering
Figure 15 illustrates an
idea I proposed in a journal article in 1977.
Let me stress that this is only one of many advanced adaptive
critic designs; you've got to go to the Handbook to get the complete
list; this is only one. (I picked this one because it's the one case where
there was a typo in the Handbook; the version here is correct.)
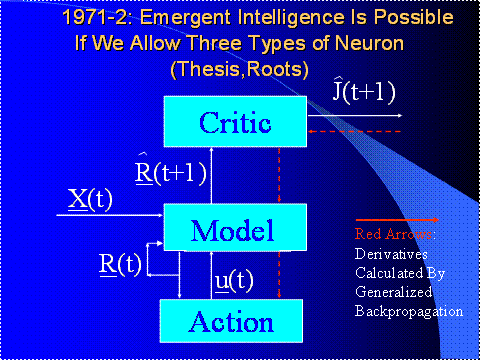
Figure
15. BAC (Version Which Uses J Output)
This is where the backpropagation algorithm really
came from, originally, in unpublished reports I wrote in 1970-72. Later I
learned how to simplify the idea of backpropagation, so people could copy it
and reproduce it. That really happened
in 1981[24], when I started playing the simple perceptron games with backpropagation
and publishing that stuff, but Figure 15 is where I really came from in the
first place.
And where did this idea come from? Believe it or not,
I developed this idea as a mathematical translation of an idea from Freud.
That's where backpropagation started. Freud had this idea. Freud was interested
in neural nets. He had to make money later on, and he regretted that he had to
make money doing stupid things, okay?
That's on the record. He started
out going to medical school, studying physiology, and what he really wanted to
do was to build a neural network theory of the human mind. He felt that he had
developed a valid theory, and he came back to that theory later in life.
His model began with the idea that human behavior is
governed by emotions. Does that sound weird?
Not if you're a human, but sometimes I almost wonder who is and who
isn't, when I see some of the theories floating around these days. At any rate,
Freud had the idea that there was something called cathexis or psychic energy
or emotional charge attached to things he called objects. According to his theory, people first of all
learn cause-and-effect associations; for example, they may learn that
"object" A is associated with "object" B at a later
time. And his theory was that there is a
backwards flow of emotional energy. If A causes B, and B has emotional
energy, then the emotional energy will flow from B back to A. And if A causes B to an extent W, then the
backwards flow of emotional energy from B back to A will be proportional to the
forwards rate. That really is backpropagation.
That really is backpropagation, and my argument is that you have to have
that. I cannot conceive of a way of
using cause and effect information without doing what Freud said. If A causes B, then you have to find a way to
credit A for B, directly. You have to
exploit the fact that you know that A causes B to the extent W. So your flow of emotional energy has to use
that number W that represents the forward association; you can't get out of
that. I see no mathematical way to get
out of it, and I've looked at a million attempts, by Grossberg and others;
there's no way to get out of that. If
you want to build a powerful system, you need a backwards flow.
Now, in mathematical terms, I can now give you a very
different interpretation of Figure 15. In Figure 15, I am properly and
dutifully following dynamic programming. (I figured this out later after
I had the design.) What I'm really doing is exactly what dynamic programming
tells me to do, which is to pick an action vector u so as to maximize J. I maximize J directly and
intelligently by calculating the derivatives of J with respect to action, any
using those derivatives. This is not
error backpropagation. This is backpropagation as a way of calculating
derivatives; I work back the derivatives with a special chain rule, the chain
rule for ordered derivatives. I work
backwards the derivatives of J with respect to U. And this is easy to implement, although
you've got to read the Handbook to get the details, since I don't have
the time here today.
So the bottom line is this: because of this argument
of Freud's, which is just about inescapable mathematically, nobody has found an
alternative to this general approach. I would predict that there must be this
kind of mechanism somewhere in the brain.
I can't see any way you could do it otherwise; I haven't seen a contrary
model that could work on that scale. And, as I mentioned before, my paper on
the cytoskeleton[5] and other papers by Dayhoff and others describe plausible
mechanisms that could implement it. It
is very plausible.
On the engineering side, there are already a number
of applications of Advanced Adaptive Critics (which I define as adaptive critic
systems which adapt an Action network based at least in part on estimated
derivatives of J with respect to u).
There is an application to the continuous production of high-quality composite
materials, which have a potential market worth many billions of dollars, et
cetera. There is an F15 application I mentioned before. Again, I have no time
for the details.
In the future, we might get into earth orbit at a
much lower cost if we can solve certain control problems; they turn out to be
optimal control problems, which classical control cannot handle very well.
Again, dynamic programming -- the appropriate classical method -- is too
expensive, but adaptive critics are not. The National Aerospace Plane office
has recently given contracts to people to use adaptive critics, to solve
optimization problems that can't be solved any other way. There is reason to believe we cannot reduce
the cost of earth orbit without using this stuff, and it's being implemented
today. A benchmark version of this control challenge is in [15].
Overall Architecture of the Brain
How does Figure 15 relate to
the brain? Figure 16 on the next page is
from a paper I published in 1987[25]. (That paper was the first to inform the
Barto-Sutton-Anderson group about the dynamic interpretation here, and about my
prior work; whatever its failings, it had a major influence on later
developments.). This figure presented a
very early approximation of what I think is going on.
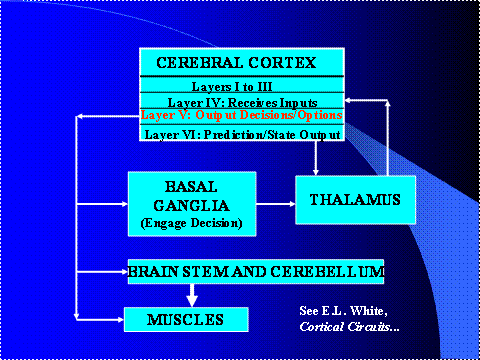
Figure 16. A First-Pass
Neurocontrol Interpretation of the Brain (From [25])
I have argued that the hypothalamus (and maybe the
epithalamus) are computing a built‑in utility function. The hypothalamus
is not the greatest center of plasticity, but it's a powerful source of primary
reinforcement. I'm arguing that the primary function of the limbic lobes is as
a critic network; we certainly know that there's secondary reinforcement in the
limbic nodes, no surprise there. (See,
for example, the classic work by Papez and by James Olds.)
I'm also arguing that the cerebral cortex includes
the function of Model network; in other words, understanding cause-and-effect
relations is its primary function. In engineering terms, that means that the
cortex is performing system identification, which includes filtering or working
memory (short-term memory) as a secondary function. This fits the recent
studies demonstrating working memory capabilities in the temporal cortex
(Goldman-Rakic) and in the frontal cortex, and the work by Barry Richmond
demonstrating the relevant kinds of lagged recurrent effects even in visual
cortex. (Because of plasticity studies, it would hard to imagine that a truly
fundamental capability like working memory could be limited to any one
architectonic area of the neocortex.)
Architecture of the Olive/Cerebellum System
Finally, in closing, I would
like to come back to the cerebellum, which is the Action network within a
complete multi-net lower-level control system. I would like to come back to the
key question which I left open earlier in this section: "How could the
lower motor system perform optimization? How could it be an adaptive critic
system?" Here, I will summarize some thoughts from [14].
Houk has done a lot of work showing that the inferior
olive sends training signals which adapt the Purkinje cells, in a way that
looks like an adaptive critic arrangement. So this is consistent with the idea
that the cerebellum is an Action net, and that the olive is a Critic directly
adapting it. What Houk doesn't talk
about is plasticity in the output layer of the network, which is a deep
cerebellar array (plus FTN cells of the vestibular nucleus). Lisberger produced
a flow chart of the FTN system for an excellent paper in Science which
nevertheless confused some people in the neural net community, who apparently
thought that the chart was a complete wiring diagram (even though Lisberger
himself discussed other connections in the text); this has led to some
nonempirical Hebbian models so unrealistic and so incomplete that the authors
should not be mentioned.
Figure 17. Flow
Chart of the FTN System From David Robinson
IO=Inferior Olive;
cf=Climbing Fiber;Pc=Purkinje Cell;gc=Granule Cell
Figure 17 is a better flow chart borrowed from Dave
Robinson, who has a new paper that will explain this better. The bottom line is
that there are cells of the vestibular nucleus (and presumably in the deep
nuclei) that also get climbing fiber input from the olive, and there's good
evidence that they train the output layer as well as the Purkinje layer. It turns out, if you look at this arrangement
mathematically, this arrangement turns out to be equivalent to backpropagating
through the action network, just like that adaptive critic architecture I was
describing. And it's neat, because it's an electronic way of doing it
that I wouldn't have thought of. The unique many-to-one architecture in the
cerebellum makes this mathematically a valid implementation of backpropagation
if you have the right training signal (a derivative signal) for the output
layer. (Strictly speaking, the Purkinje-to-deep connectivity is more like
850-to-35, according to Pellionisz, rather than many-to-one in a precise sense;
however, this is no problem, if we assume that the 35 related deep cells are
representing a common variable, using multiple channels to permit greater
precision.)
But how do you get this training signal from the
olive? If you read things like Houk and
Barto, they begin to be a little
incoherent when it comes explaining how the olive learns to give a training
signal specific to a given action variable. Now it turns out, on the neurocontrol side,
that there is one and only one class of working design (we now know) that
yields output in a powerful way that you can use to train individual action
nodes. And it's this weird thing here
(in Figure 18)...and you have this particular kind of critic network that
outputs training signals to an action network, and what do these things
represent? They represent the
derivatives of J with respect to the individual, specific action variables.
Figure
18. Example of an ANN Neurocontrol Design
Now, I don't think the cerebellum is doing this, I've
matched Figure 18 to the cerebellar circuit and it doesn't fit. But it is very
clear to me from what is going on here that those olive signals must represent
the derivative of J with respect to u.
Is there any way that that could happen?
Well, it turns out the cerebellum suggests a new
design different from what we've had before, that is still understandable in
terms of the same mathematics. The basic idea is that the olive output has to
be trained in one of two ways:
either (1) there's a local
target that tells each climbing fiber what the derivatives of J with respect to u are. In this arrangement, the
point is that the olive is anticipating a slower system. The need for speed
explains why it is good to have an olive; that's why you don't just use the
target itself to train the cerebellum.
(2)
The other hypothesis is that a lot of complicated learning is going on
inside the olive (perhaps like
Figure 18, for example). But you can't
do that unless you have an efference copy of the action vector u.
So there are only two possible hypotheses. One is that there is some kind of
backpropagation along the climbing fibers -- either in the climbing
fibers or along them -- so that somehow a target which is local to the
action region gets back to train the olive.
That's one possibility; it's pretty crazy, but you could cut the fiber
and find out. The other possibility is
that the fibers that go from the deep nuclei back to the olive provide a
complete efference copy which is used in training the olive. If that is true, then you cut those
fibers and eliminate plasticity in the olive (or modify it substantially).
You can do the experiment. I can't. I hope that you
do. Thank you.
References
[1] W.Nauta and M.Feirtag, Fundamental Neuroanatomy. W.H.Freeman,
1986.
[2] P.Werbos, The Roots of Backpropagation: From Ordered
Derivatives to Neural Networks and Political Forecasting, Wiley, 1993.
[3] P.Werbos, "Neural
networks and the human mind: new mathematics fits humanistic insight," in Proc. Conf. SMC, IEEE, 1992. An updated version is in [2].
[4] P.Werbos, "Quantum
theory and neural systems: alternative approaches and a new design," in
K.Pribram, ed.,
Rethinking
Neural Networks: Quantum Fields an Biological Evidence, INNS Press/Erlbaum,
1993.
[5] P.Werbos, "The
cytoskeleton: why it may be crucial to human learning and neurocontrol," Nanobiology, Vol.1, No.1, 1992.
[6] M.Baudry and J.Davis,
eds, Long-Term Potentiation: A Debate of
Current Issues, MIT Press, 1991.
[7] T.Smirnova, S.Laroche,
M.Errington, A,Hicks, T.Bliss and J.Mallet, "Transsynaptic expression of a
presynaptic glutamate receptor during
hippocampal long-term potentiation," Science,
Vol. 262, p.430-436,
October 15, 1993.
[8] J.Dayhoff, S.Hameroff,
R.Lahoz-Beltra and C.Swenborg,"Intracellular mechanisms in neuronal
learning: adaptive models", IJCNN92 Proceedings, IEEE, 1992.
[9] F.Fukamauchi, C.Hough
and D.Chuang, "m2- and m3-Muscarinic Acetylcholine receptor mRNAs have
different responses to
microtubule-affecting drugs," Molecular
and Cellular Neurosciences, Vol. 2, p.315-319, 1991.
[10] C.Hough, F.Fukamauchi
and D.Chuang, "Regulation of b-adrenergic receptor mRNA in rat C6
glioma cells is sensitive to the state
of microtubule assembly," Journal of
Neurochemistry, Vol. 62, No.1, 1994.
[11] G.Stuart and B.Sakmann,
"Active propagation of somatic action potentials into neocortical
pyramidal cell dendrites," Nature,
Vol. 367, No. 6458, p.69-72, Jan. 6, 1994.
[12] D.Gardner,
"Backpropagation and neuromorphic plausibility," WCNN93 Proceedings, INNS Press/Erlbaum, 1993.
[13] D.Gardner, The Neurobiology of Neural Networks, MIT
Press, 1993.
[14] P.Werbos and
A.Pellionisz, "Neurocontrol and neurobiology," In IJCNN Proceedings, IEEE, 1992.
[15] D.White and
D.Sofge,eds, Handbook of Intelligent
Control: Neural, Fuzzy and Adaptive
Approaches. Van Nostrand, 1992.
[16] D.C.Tam, personal
communication and "A new conditional correlation statistics for detecting
spatio-temporally correlated firing patterns in a biological neuronal
network," WCNN93 Proceedings,
INNS Press/Erlbaum, 1993.
[17] W.Miller,R.Sutton and
P.Werbos,eds, Neural Networks for Control.
MIT Press, 1990.
[18] P.Werbos,
"Supervised learning," WCNN93
Proceedings, INNS Press/Erlbaum, 1993.
[19] P.Werbos, "Elastic
fuzzy logic: a better fit to neurocontrol and true intelligence," Journal of
Intelligent and Fuzzy Systems, Vol. 1, No. 4, 1993.
[20] K.Pribram and M.Gill, Freud's Project Reassessed, Basic Books,
1976.
[21]
K.Pribram,"Familiarity and novelty: the contributions of the limbic
forebrain to valuation and the
processing of relevance," in D.Levine
and S,Leven, eds, Motivation, Emotion and
Goal Direction in
Neural Networks, Erlbaum, 1992.
[22] P.Werbos,
"Backpropagation through time: what it does and how to do it," Proceedings of IEEE, October 1990 issue. A slightly updated version is in [2].
[23] P.Werbos,
"Neurocontrol: where it is going and why it is crucial," in I.
Aleksander and J.Taylor, eds,
Artificial
Neural Networks II.
[24] P.Werbos,
"Applications of advances in nonlinear sensitivity analysis," in
R.Drenick and F.Kozin, eds,
Systems
Modeling and Optimization: Proc. of the 1981 IFIP Conf., Springer-Verlag,
1982. Reprinted in [2].
[25] P.Werbos,
"Building and understanding adaptive systems: a statistical/numerical approach
to factory automation and brain
research, IEEE Trans. SMC, Jan.-Feb.
1987.
Additional Points After Publication
1. The exploratory project
by Houk, Cockberger and Alford was not successful. They were unable even to
attempt the search for plasticity in olive cells, because they were unable to
create a viable culture of these cells. Following up on the collaborative work
of Houk and Barto, assuming a Barto-Sutton-Anderson Critic model, they felt it
was most critical to have a co-culture of olive cells with spinal cells (to
supply pain inputs, to provide the U input necessary to the training of the
Critic.). I suggested that cerebellar cells (preferably deep) be added as well,
because the more sophisticated critic models I claim to be essential would also
requirte such cells. I have argued that the simple Barto-Sutton-Anderson design
simply does not make sense in this application. (This, despite the fact that I
published the same simple critic adaptation rule in 1977, 6 years prior to the
Bart-Sutton-Anderson paper; in that 1977 paper, however, I pointed out the
weaknesses of that method when dealing with highly multivariate systems. By
engineering standards, the cerebellum is incredibly multivariate.)
Nevertheless, they never even attempted a co-culture including cerebellar
cells.
In their work, however, Houk and Hockberger
did cite a successful co-culture of olive and cerebellum cells by J. Mariani of
2. Since this was published,
I have had occasion to look morte carefully at the work of
It should be possible to
prove something analogous to the Bel;l’s Theorem in physics, pointing towards
specific experiments which unambiguously are inconsistent with the ordinary
postulated “forwards” flows of information in the learning process. There are
truly exciting possibilities here which are only just now coming into focus.
3. Naturally there has been
great progress in implementing some of these designs in engineering since this
paper was published. A more up-to-date
understanding of the entire neurocontrol situation may be found in chapter
F1.10 of the Handbook of Neural Computation from Oxford U. Press, Fiesler et al
eds, 1995. Some recent results in more brain-like adaptive critic architectures
are reviewed in my paper in 1994 Workshop
NN/FS/ES/VR, edit by M.Padgett of Auburn U. (who may have advance copies),
published in 1995 by SPIE of Bellingham, Washington.
A more specific discussion
for engineers of how they can play a critical role in engineering-biology
collaboration, and how, is in my paper in the proceedings of the 1994 Yale Workshop on Adaptive and Learning
Systems, available from the editor, Prof. K.S. Narendra at the Electrical
Engineering Department of Yale University.
4. Grossberg has pointed out
that certain limitations in the Klopf architecture would make it intrinsically
unable to account for more complex examples of classical conditioning. He
argues that an “expectations” subsystem is essential. I fully agree with
Grossberg’s position. The more recent Critic designs cited here fully account
for that concern. In particular, in postulating that the thalamo-cortical
system is adapted primarily as a system identification or expectations system,
I am hypothesizing that a rather large chunk of the brain is dedicated to that
task. Nevertheless, it is reassuring that a very simplified version of this
class of model does perform well relative to more classical models, for the
kinds of experiments that have been the focus of animal behavior modelling in
the past.