Abstract
Many people say that
neurocontrollers should never be used in real-world applications until we
possess firm, unconditional stability theorems for them. But such stability
results do not exist for any real-time O(kn) controllers, either
neurocontrollers or traditional adaptive controllers, even for the general case
of controllable plants X
governed by ¶t X = AX+Bu where
A and B are unknown. This paper explains key ideas from a longer paper which
discusses this problem of “universal stability” (in the linear case) and
proposes a new solution. New forms of real-time “reinforcement learning” or
“Approximate Dynamic Programming” (ADP), developed for the nonlinear stochastic
case, appear to permit this kind of universal stability. They also offer a hope
of easier and more reliable convergence in off-line learning applications, such
as those discussed in this session or those required for nonlinear robust
control. Challenges for future research are also discussed.
This paper will try to explain some key ideas from a longer paper [1], which discusses the relations between classical control, modern control and neural network control in a more general way. In particular, this paper will focus on the new learning designs mentioned in the Abstract.
Cost and Stability In Adaptive
Control
Full-fledged adaptive control or real-time learning control is still rare in practical applications. I would claim that this is partly due to the stability problems mentioned in the abstract – problems which we can now overcome.
But before I explain this, I need to say something about what I mean by “full-fledged real-time learning control.”
For full-fledged real-time learning, I require, of course, that the weights or parameters of the controller are adapted in real-time, but that is not enough. I also ask that a certain cost constraint be followed, which guarantees that the calculations can really be done in real-time, even for massive control problems (as in the brain!).
The new methods given in [1] meet the usual tough standards one would expect for a true neural network design. Given a network with n outputs and k connections
per output (roughly), it costs on the order of kn calculations
to run the network. It costs about the same to run backpropagation through such a network. The new methods in [1] involve similar cost factors; they don’t involve any
T-period lookahead (which costs O(knT) calculations), and they don’t involve any “forwards propagation” or “dynamic backpropagation” (which costs at least O(kn2) calculations).
In classical adaptive control, Astrom and Wittenmark [2]
describe ways that one could achieve universal stability, if one performs an explicit solution of complex Riccati equations over and over again in every time period.
Those are important results, but they are not enough to meet our goals here, because of the cost factor.
The classic text of Narendra and Annaswamy [3]
describes at great length the historic effort to achieve
universal stability in true adaptive control, in the linear case. It also describes the very large gap between present designs and that goal. In a series of more recent papers (cited in [1]), Narendra has become more and more emphatic about the limitations of Indirect Adaptive Control (IAC), which, he argues, is the best of the existing designs.
Even in the linear case, IAC requires (for stability) that the “unknown” plant must actually have a known kind of structure. It doesn’t exactly require that you have to know the sign of every element in the matrices A and B – but you have to know things just as difficult. And even then, A and B must have certain special properties for IAC to work at all. In the majority of real-world plants, these tough restrictions are not met. Thus even in the linear case, adaptive control tends to go unstable in most real-world plants. (There are a few notable exceptions.) Naturally, the neural network version of IAC also tends to have stability problems, and problems of slow transient response, despite its enormous popularity.
Given these problems, it is not really surprising that true adaptive control has not lived up to its potential in real-world applications. Most industry users now rely on a variety of tricks [1,4] to obtain adaptive sorts of capabilities from controllers designed or trained off-line.
Figure 1 illustrates how IAC works, for the general, neural network version. The basic idea is simply that the weights of the Action network are trained so as to minimize the tracking error at time t+1. See [1] and the papers of Narendra for the exact equations.

Figure 1. Indirect Adaptive Control
Can ADP Save Us?
From an intuitive point of view, there is an obvious explanation for why IAC can go unstable. In Figure 1, there is simply no machinery present to “tell” the Action network to avoid actions which lead to large tracking errors beyond time t+1! The design is purely myopic, purely short-sighted in time. See [1,4] for more discussion of this problem.
The obvious solution is to modify IAC, to make it try to minimize tracking error summed over all future times, not just time t+1. To do this, we can simply replace IAC by the Approximate Dynamic Programming (ADP) design shown in Figure 2. The adaptation of the Critic network in Figure 2
requires the use of a user-specified utility function, U, not shown. If we simply choose U to be the same measure of tracking error shown in Figure 1, Figure 2 will have the effect of minimizing the sum of tracking error summed over
all future time.
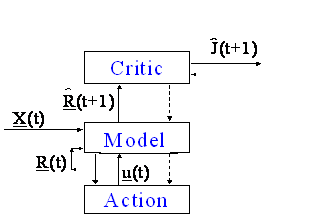
Figure 2.
HDP+BAC (an ADP Design)
This design was first specified in detail in my Sept. 23, 1972, thesis proposal to
Heuristic Dynamic Programming (HDP) refers to the general method I proposed to adapt the Critic network in this design. The goal is to adapt the parameters W in the network J(R,W) so as to make J obey the Bellman equation, the basic equation of dynamic programming, which may be written in the following form:
J*(R(t))= Min{u}(U(R(t),u)+<J*(R(t+1)>/(1+r)),
(1)
where J* is the true function which we are trying to approximate with the Critic, where U is the user-supplied utility function, where “r” is a user-supplied interest rate
(usually zero here, except when useful as a kind of convergence gimmick), where the angle brackets represent expectation values, and where I choose minimization instead of maximization because the goal here is to choose u so as to minimize tracking error over future time.
When the tracking problem can be solved at all (even allowing for some delay), then the J* function will exist.
More precisely, when the process to be controlled is “controllable” in the very broad sense described by Stengel [5] and others, J* will exist. For a deterministic system
(like ¶tX = AX+Bu) and a reasonable choice of U, J* is guaranteed to be a Lyapunov function; in other words, it is guaranteed to stabilize the system.
The obvious conclusion is as follows: if our neural network J(R,W) converges to the correct function J*(R), for any controllable system ¶tX=AX+Bu, then it should stabilize that system. This design should provide universal stable adaptive control in that case, if the Critic converges correctly. In the linear case, we can pick the form of J(R,W) to be a general quadratic function over X, which guarantees that J(R,W) will match J* exactly for some choice of the weights W. But this leads to a key question: will HDP always converge to the right weights W, at least for controllable systems?
In studying this question last year, I was surprised to find that HDP does not always converge in a stable way to the right weights, even for a linear deterministic process. Furthermore, none of the consistent previous methods of ADP or reinforcement learning would do so either. (See [1] for an exhaustive survey and discussion, discussing DHP, GDHP, TD, ADAC, Q, Alopex, etc.) There was only one exception – a method mentioned in passing in a tech report from Klopf’s group at Wright-Patterson, for which I could find only one record of an implementation; in his PhD thesis, Danil Prokhorov reports trying that method, and observing very poor results, due to some obvious strong noise effects. (See [1] for details.)
Crudely speaking, there are two general strategies for how
to make equation one “approximately true,” each discussed at length in [1]. In HDP, one adjusts the weights W so as to make J(R(t)) come closer to the right-hand side of equation one, without accounting for the way in which changing weights would change the right hand side as well. In a “total gradient” approach (HDPG [1]), one simply minimizes the square of the difference between the left hand side and the right hand side, accounting for changes on both sides. In [1] (and in a previous paper), I showed that the equilibrium value for the weights will be correct, using HDP, but incorrect, using HDPG, for any linear stochastic plant. This tells us that HDPG is unacceptable as a general-purpose ADP method for the stochastic case. But even though HDP gives the right equilibrium value for the weights, it turns out that this equilibrium will not be a stable equilibrium, in general, in the strict sense required here.
Tsitsiklis and Van Roy [6] did show that a modern form of “TD” (HDP rediscovered) does converge to the right weights in general, for systems which have a kind of “normal” training experience. But my goal here is to provide a stronger, more unconditional guarantee of stability. HDP does not provide that stronger guarantee.
This is proven in excruciating detail in [1].
This led to the question: what can we do about this? Should we give up the search for universal stable adaptive control
even in the linear deterministic case? Or does the solution of that problem require the use of methods which are inherently limited to that special case, and irrelevant to the larger problem of survival in a nonlinear stochastic world?
Fortunately, the answer to both questions turns out to be “no.”
New Critic Designs
Once the reasons for instability are explained, there are actually a number of methods for overcoming them. Thus in [1], I first describe four variations of HDP to solve the problem (section 9.1); I then describe two variations for each of the four (section 9.2); and finally (section 9.3) I describe how similar variations exist for Dual Heuristic Programming (DHP) and Globalized DHP(GDHP).
Considerable research will be needed to decide which
variants work best and when, and whether there is any possibility that the brain uses or needs anything like this degree of stabilization.
A critical task for future research is to repeat the same kind of painstaking step-by-step development of total system stability theorems here that Narendra performed long ago for IAC [3], but without the same restrictions. I would guess that GDHP0 (defined in section 9.3 of [1]) would be the most convenient starting point for such efforts,
in part because one can avoid the need for interest rates.
However, to get the basic idea of one of these methods, it would be easiest to consider HDP0. HDP0 is a variation on the following special case of HDP.
In a common form of HDP, we always start from some initial state, R = R(t) at time t. This may be a currently observed state of the external world, or a state imagined in some kind of internal simulation. Before we adapt the weights Wij, we wait until we have a corresponding value for R(t+1); we may obtain R(t+1) either by observing the actual state of the plant at time t+1, or by exercising a stochastic simulation model R(t+1)=f(R(t), u(t), e(t)),
where e is a vector of random numbers. After the value of R(t+1) is available, we update the weights by:
![]() (2)
(2)
where:
e =
U(R) + J(R(t+1))/(1+r) - J(R, W) (3)
Thus:
![]() (4)
(4)
In HDP0, we must also train a deterministic neural network model f’, to try to predict R(t+1) as f’(R(t),u(t)). The neural network f’ would be a best-guess forecasting model, not a true stochastic model. To adapt the weights W, we still use equations 3 and 4, except that we replace the last term in equation 4 by:
![]()
(5)
Both in equation 4 and in equation 5, all the calculations can be done inexpensively by a proper use of backpropagation.
Both for equation 4 and equation 5, the weights reach equilibrium whenever we meet the correct statistical condition, <e>=0. Thus strange and ad hoc as equation 5 may seem to be, at first, it is just as precise in its equilibrium requirements as HDP proper, even in the nonlinear stochastic case. However, the search direction used in equation 5 is much closer to being a total gradient than is the search direction for equation 4; that substantially reduces the chance of the kind of instabilities in HDP discussed in [1]. In particular, for the linear deterministic case, equation 5 yields the same results as HDPG which, as proven in [1], obeys a very strong test of stability (quadratic stability) in that case.
Again, this is only one of many methods described in (1).
These methods lead to a number of practical possibilities and further research opportunities, described above in this paper. Those in turn are still only one of the very important
streams of research needed to bring us in the end to truly brain-like artificial intelligent systems [7].
References
1. P.Werbos 1998, Stable Adaptive Control Using New Critic Designs, xxx.lanl.gov/abs/adap-org/9810001
2. K.Astrom and B.Wittenmark, Adaptive Control,
3. K.Narendra and A.Annaswamy, Stable Adaptive Systems,
4.Werbos, Neurocontrollers, in J.Webster, ed, Encyclopedia of Electronics and Electrical Engineering, Wiley, 1999
5. Richard F. Stengel, Optimal
Control and Estimation,
6. J.Tsitsiklis &B. Van Roy, An analysis of temporal-difference learning with function
approximation, IEEE Trans. Auto. Control, Vol. 42, No. 5, May 1997
7. P.Werbos, Brain-like stochastic search: A research challenge and funding opportunity, Proc. Conf. Evolutionary Computing (CEC99), IEEE, 1999.