Neurocontrollers
In
J. Webster, Ed., Encyclopedia of Electrical and Electronics Engineering, Wiley,
1999
-----------------------------
*
The views expressed herein are those of the author, not those of his employers,
although the work was written on government time.
Neurocontrol:
An Overview for the Practitioner
What is Neurocontrol?:
The General Approach
Neurocontrol is a new branch of engineering practice and research, which first came
together as an organized field in 1988 (1).
Actually,
the philosophy behind neurocontrol dates back much
earlier than 1988. Norbert Wiener (2) originally defined “cybernetics” as a
kind of unified theory of control and communication in the animal and the
machine. Neurocontrol tries to implement Wiener’s
original vision, by building control systems or decision-making systems which
can learn to improve their performance over time, and can use a parallel
distributed kind of computing hardware similar to what the brain uses.
For
a long time, many engineers have been intrigued by the idea of developing an
“all purpose black box controller,” which could be plugged into any
application. The box would have wires going out to the actuators and other
controllers, wires coming in from sensors, and a special wire coming in from
the “utility module” -- a system which monitors and measures the overall
success of the controller, based on criteria which must be supplied by the
user. The engineer using the box would have to worry about providing the right
inputs and outputs, but the black box would figure out all the rest, based on
learning. It would learn by itself how to maximize utility over future time,
even if that requires developing a complex strategy in order to reach a
desirable state. Many people now define “reinforcement learning” as the problem
of designing this kind of black box (1,3), illustrated
in Figure 1.

Figure 1. Reinforcement Learning
System (RLS)
Reinforcement
learning systems do exist today -- but they vary greatly in quality, and they
all have notable limitations. Still, there is a pathway now defined for future
research which does seem to point the way, in concrete terms, to the
development of future reinforcement learning systems which really could
replicate the high level of intelligence and flexibility that exists in the
brains of mammals. (Actually, performance is usually better with reinforcement
learning designs in which the utility function is a known differentiable
function of the other inputs. Such modified designs may even be more plausible
as models of the brain. (4,61)). There has been considerable reserach demonstrating links between the reinforcement
learning designs which are useful in engineering, and the brains and behavior
of various mammals (e.g, (4), (62-64)); however, new
interdisciplinary partnerships between engineers and biologists will be crucial
to a deeper understanding of these links.
As
a practical matter, most control tasks today do not require full-fledged brains
to perform them. There is a complex “ladder” of designs available in neurocontrol, rising up from simple designs of limited
power through to very complex, more brain-like designs. Roughly speaking, they rfanghe in scope from designs which use neural networks to
“clone” the observed behavior of an existing expert, through to designs for
tracking setpoints or desired “refernce
trajectories,” through to full-scale designs for optimization over time.
Effective engineering groups usually start out by implementing the simpler
designs, in general-purpose software, and then systematically climb up the
ladder, one step at a time, to expand their capabilities and to reduce their
costs in coping with ever more difficult applications. The key to
effectiveness, then, is to know where one is on the ladder at any time,
and to know what the choices and benefits are for the next step up. This
requires making some effort to map out, decode and unify a rather complex,
fragmented literature, drawing from many different disciplines which use
different terminology. This chapter will try to help the reader in this task.
Furthermore,
in practical terms, real-time learning or “learning on the fly” is not always
the most effective way to solve a control problem. We usually have three kinds
of information about the plant available to us, when we try to solve a control
problem: (1) true prior information, such as a physical model of the
plant to be controlled; (2) a database of datastreams
for the sensors and actuators in the plant, datastreams
which could be based on physical recordings or on simulation; (3) the actual
current stream of data from the plant which we are now controlling in real
time. Statistical principles (5) suggest that the best controller will always
be the one which combines all three sources of information in an optimal
manner.
Roughly
speaking, traditional control uses only the first source of knowledge in
designing the controller. (Of course, the controller itself normally does
respond to current sensor input, after it has been designed and put into
operation.) “Offline learning” in neurocontrol uses
the second source of knowledge. “Real-time” learning in neurocontrol
(and adaptive control (6,7)) uses the third. The challenge is to develop all three
capabilities, and then find ways to blend (or select) all three, across a range
of applications. The simplest applications really do involve the control
of a physical plant, like a furnace. The more complex applications may really
involve making decisions so as to optimize or influence a
much more complicated environment, like a factory or an entire economy.
Relations With Other Forms of Control
In
the 1980’s, neural network people and control theorists often expressed extreme
emotional judgments about the strengths and weaknesses of neurocontrol
versus conventional control. For example, some neural network people argued
that neural networks could solve problems that mere mathematical approaches
could not. Some control theorists argued that the reverse was true, and that
all users of neural networks must be black box black magicians. Rhetoric like
this has lingered on in some quarters, but a more concrete and reliable
understanding has begun to emerge in the mainstreams of both fields.
The
convergence actually began in 1988, in the National Science Foundation (NSF)
workshop which first brought together people from different parts of this
field, and injected the term “neurocontrol” (1). In
that workshop, it became clear that the major designs being used in neurocontrol can actually be considered as special cases of
more general learning designs within the field of control theory.
(Unfortunately, some people associate “control theory” only with the simplest
form of control, like thermostats; control theory in the broadest sense is
really the theory of decision and control, including simple systems like
thermostats, but also including nonlinear optimal control, stochastic control
and so on.)
To
understand the concrete implications of this situation, consider the following
analogy. The general learning control designs used in neurocontrol
can be compared to circuit boards performing a higher-level function,
containing some empty sockets where something has to be plugged in. For example,
most of these learning control designs contain “sockets” where you must plug in
some kind of general-purpose system which can learn to approximate nonlinear
functions. Most people simply plug in
some sort of artificial neural network (ANN) into these sockets. But you could
just as well plug in an elastic fuzzy logic module (8, ch.13), a Taylor series
module, a soft gain scheduler, or any differentiable system of user-specified
equations (9; 3, ch. 10) into any one of these
sockets, if you know how to plug in all the associated information
required (3, 8, 9).
The
learning control design itself -- the “circuit board” -- does not really
contain any neural networks. Therefore, it may be slightly misleading to call
these higher-level designs “neurocontrollers.” It
would seem more precise to call them learning control designs or intelligent
control designs. However, the terms “intelligent control” and “learning
control” have been used in the past to refer to a wide variety of other
designs, of varying degrees of real intelligence. In this article, the
term “learning control” will refer to the specific types of generalized
learning control design which are used in the neural network community;
however, this is not standard terminology.
In
practical applications, then, the design process here actually works at three
levels. On the lowest level, we must decide which subsystems to plug in -- the
specific ANNs or other modules to perform function approximation or prediction or whatever. At the
middle level, we must choose one or more higher-level learning designs, to
perform general higher-level tasks like cloning a human expert, tracking a
desired trajectory or optimizing a performance measure. At the highest level,
we must map these higher-level tasks into a real application, which often
requires a variety of tasks to be performed, in parallel or in sequence.
Unfortunately,
many neurocontrol papers talk at length about their
choices on one of these levels, without doing justice to the other
levels. Some papers, when evaluating neurocontrol, confuse
the costs and benefits of the learning design with the costs and benefits of
particular subsystems; in fact, in some cases, they restrict the analysis to
only one type of ANN. One of the worst common mistakes is to confuse the pros
and cons of backpropagation -- a very general technique for calculating
derivatives (9) and adapting networks -- with the pros and cons of a particular
class of ANN, which is properly called the Multilayer Perceptron (MLP) but
often improperly called a “backpropagation network.”
Benefits and Capabilities
of Learning Control Designs
Because
the design process operates at these three levels, it does not make sense to
ask what the benefits are of neurocontrol as such.
Instead, we can ask what the benefits are for using these learning control
designs, in general, at the middle level of the design process. Then,
when we need to fill in the sockets, we can ask what the benefits are of using
specific types of ANNs instead of other possible
subsystems. In many applications, at some stages of development, it makes sense
to use a mixture of subsystems, including some ANNs
and some other types of subsystem..
The
benefits of learning control in general are fairly straightforward. In
traditional design approaches, controllers are usually developed based on
models before the plant is even built. Then, once a prototype is built, and the
control does not actually work as intended, there is a long and laborious
period of testing, remodelling, and tweaking. In the
aircraft and manufacturing robotics areas, many experts estimate that 80% of
the costs of the entire system development effort come from this tweaking
stage. If one could replace tweaking by a more automated process of learning,
one could reduce these costs substantially, and accelerate the development
schedule. In some
cases -- as with novel high-performance aircraft -- the reduction in tweaking
could also mean a reduction in the need to crash a few prototypes during the
development process; such crashes were once a normal and unavoidable part of
the development process, but are becoming less and less acceptable today.
Learning
control can be used in two major ways to reduce the need for tweaking after the
development of traditional controllers:
(1) Given a flexible enough
control structure, initialized to something like a traditional controller, one can train the controller to optimize
performance over a wide range of possible assumptions, in offline
learning. For example, one can use a simulation model to generate multiple
streams of training data, but with different parameters or couplings assumed in
each stream of data. When first proposed in 1990 (10), this general approach
was called “learning offline to be adaptive online.” Since then, Ford Research
has extended the approach in a wide range of applications (e.g. 11,12), and called it “multistream
learning.” The success of this approach depends heavily on the flexibility of
the control structure and on how well it is initialized. Controllers developed
in this way are now the only affordable mechanism which have
demonstrated that they can achieve ultralow emissions
on road-tested cars from a
(2) True real-time learning
permits adaptation to the actual real-world plant. For example, in aviation,
one might use real-time learning much as a human pilot does, by gradually
extending the envelope of safe operation from low speeds to higher speeds,
etc., while always monitoring how close the system is to the edge of that
envelope. In this case, the trick is to move out far enough that one is
learning something, but not so far that one is in danger.
Actually,
there are many variants of these approaches, and a very complex connection to
formal control theory. For example, in automotive control, one could pool
actual data from a number of real cars, for use in “offline multistream”
learning. Likewise, there is room for more systematic efforts in deciding how
to generate the multistream training data. In one
version, one could even train an “adversary neural network” to control the
random disturbances and parameter uncertainties, and to try to destabilize the
proposed controller (neural or nonneural); this would
be a way of implementing the notion of “robust stability as a differential game”,
which is fundamental in modern control theory (13). One way to evaluate the
actual stability of competing controllers and competing engineers may be to
offer them each the challenge of destabilizing each other’s controllers,
subject to various limitations on how much disturbance they are allowed to
introduce. Alternatively, the offline learning techniques developed in neurocontrol can be used as an efficient numerical
technique for finding the solutions to a nonlinear stochastic optimization
problem -- which is also an important element of robust control(13).
Finally, it should be possible in principle to link these kinds of
learning-based designs to actual Computer-Aided Design (CAD) tools and simulations, in order to
permit something like “design for controllability” or “design for dynamical
performance”; this could someday be extremely useful in reducing the number of
generations required for certain kinds of design processes (e.g., for fuel cell
automobiles), but little work has been done so far along these lines.
The
discussion so far has described the benefits of these learning control designs in
general. But there is a wide variety of designs available, intended to
perform different tasks, with a variety of different applications and benefits.
These designs will be described in more detail later on. For now, in summary,
there are three broad classes of designs forming a kind of ladder from simplest
to most complex:
(1) Cloning designs. These
designs permit you to emulate the actual behavior of an existing expert
controller, such as a human being or an accurate but expensive automatic
controller. Unlike the usual expert systems, these designs imitate what
the human does rather than what he or she says.
(2) Tracking designs. These
designs permit you to track a desired setpoint (like
desired temperature, in a thermostat) or a desired reference trajectory (e.g.,
desired movement of a robot arm) or a “reference model” whose function is to
output a desired trajectory.
(3) Designs to perform multiperiod optimization, explicitly or
implicitly. The explicit designs tend to be simpler to implement, and more
exact, but computationally more expensive and less capable of coping with
random disturbances. The implicit designs are sometimes called “reinforcement
learning,” and have strong connections to what we see in the brain (14). In
some applications, it is best to use a hybrid, where the explicit methods
provide a short-period look-ahead and the implicit methods account for payoffs
or results beyond that period (15).
Sometimes
it is very difficult to find the best controller simply by using an
optimization method, starting from neural networks initialized with random
weights. It is often best to take a step-by-step learning approach. In
this approach, one first trains a controller to solve a relatively simple task.
The final version of that controller, after training, is then used as the initial
version of a controller trained to perform a more difficult task. In any
kind of learning system, the initial structure of the controller -- the
starting point -- plays an important role in deciding what can be learned.
For
example, Accurate Automation Corporation -- AAC (16) -- visited Wright
Patterson Air Force Base a few years ago, to propose the use of optimizing neurocontrol to help solve some of the pervasive weight
problems expected with the National Aerospace Plane, NASP. (NASP was intended to be a prototype of an
airplane which could reach earth orbit, as an airplane, at airplane-like
costs.) But they were told that it took millions of dollars even to develop a
controller able to stabilize the craft -- let alone optimize it --
following their nonlinear model of the vehicle.
AAC
then created a video game to run on Silicon Graphics, to simulate the NASP
model, but at a speed slow enough that a human being would have some hope of
stabilizing it. Many humans played the game, but only a few were able to
stabilize and land the craft consistently. AAC recorded the behavior of those
successful humans in the game, and simply developed a neural network clone of
their behavior patterns. This neural net could then stabilize the aircraft, in
all their tests, and -- unlike the humans -- could run at electronic speed. The
resulting network could then be used, in principle, as the initial value of the
controller for a neural optimization scheme.
Based
in part on this very rapid success, AAC -- a small neural network company --
became a prime contractor on the NASP program, and then went on to play the
lead role in the follow-ons to NASP, the LoFlyte program and the HyperX,
where neurocontrol is planned to play a central role.
Of
course, step by step learning is not the only way to define the starting point
for a learning controller. For the first task to be learned, one may start out
by using neural networks with random weights, or weights selected on an
intuitive basis. Or one may define the total control system to equal a
previously designed traditional controller plus a simple neural network.
Or one may use a neural network clone of a pre-existing traditional controller.
Or one may use a set of fuzzy IF-THEN rules encoded into an elastic fuzzy logic
module (8). (Fuzzy IF-THEN rules are rules like “if the engine is hot and the
pressure is rising, then turn down the fuel intake.”) The choice really depends
on what kind of information is readily available, and on the requirements of
the particular application. One can never guarantee that a nonlinear learning
system of significant size will find the globally optimal strategy of action;
however, one can generally expect it to improve upon the best of what is
tried when initializing the system.
The
difficulty of finding the global optimum, and the value of
careful initialization, vary greatly from application to application.
Unfortunately, the conventional wisdoms about these issues often reflect past
traditions and habits rather than the real needs of particular applications.
Learning Versus Feedback Versus Adaptation
The
previous section discussed the benefits and capabilities of learning control in
general. The section after next will discuss the benefits of neural networks
versus other subsystems, within the framework of learning control. But
first, this section will begin to round out the discussion of learning control
in general, by discussing the relation between learning, feedback
and adaptation, which tends to be confusing even to researchers in the
field.
In
control, in general, there is a ladder of five major categories of design, in
order:
(1) Static controllers. For example,
the valve controller on an ordinary gas stove is a static controller. After you
turn the dial, the system simply injects gas at a fixed rate. Some people put
timers on top of static controllers (as in some gas ovens), but the basic
principle remains the same: the control action is specified completely in
advance, without any use of sensor input other than a clock.
(2) Feedforward controllers.
In a chemical plant, the controller for one valve may actually respond to the
flow of other gasses or liquids coming into the reactor. In a
feedforward controller, the control action at any time, u(t),
may depend on some sensor inputs -- but not on inputs which measure how
well the controller is performing. Static controllers or feedforward controlers are often referred to as “open-loop control.”
(3) Fixed feedback controllers.
Feedback control, as a practical tool in engineering, dates back at least to
James Watt’s flywheel regulator, crucial to the first successful operation of
steam engines, which in turn were crucial to the industrial revolution. The
modern, more mathematical concept of feedback control emerged much later,
particularly in the seminal work of Norbert Wiener (2). To explain this
concept, Wiener discussed several simple examples such as the everyday
thermostat. In the thermostat, there is a feedback from a thermometer to
the controller which turns the furnace on and off. When the temperature is too
high, the furnace is turned off. In other words, there is a sensor which
measures the actual value of the variable (temperature) which we are
trying to control. The control action is specified as a function of that
sensory reading. In fixed feedback control, the controller has no memory;
its behavior is fully specified in advance as a function of all the sensor
inputs (and perhaps of its own past actions) at specified times. For example,
the function may depend on sensor readings at the present time, t, and on
readings at times t-1, ..., t-k,
for
some k.
(4) Adaptive controllers.
Adaptation changes the behavior of a controller, so as to account for
changing conditions in the plant being controlled. For example, a good human
driver knows how to adapt when roads become slippery due to rain. Even
if the driver cannot see how slippery the road is in different places,
he can sense how the behavior of his car is changing, and adapt accordingly.
Later, when the rain dries out or he enters a dry patch, he has no trouble in
returning to his old pattern of driving. In engineering, there are many
situations which require adaptation, such as changes in the mass and location
of a load to be carried (17), changes in the friction of a moving part, changes
in the atmosphere, wear and tear, and so on. In formal terms, adaptation
tries to adjust the control rule so as to account for variations in the
plant which cannot be observed directly, and which typically (but not always)
vary slowly with time.
(5) Learning controllers.
Learning control tries to build systems which, like
the brain,
accumulate knowledge over time about the dynamics of
the plant to be controlled -- or, more generally, about the environment which
the controller lives in, and about strategies for coping with these dynamics.
For example, an inexperienced driver may not know how to change his
driving behavior during a rainstorm. This causes many crashes. Over time, a
driver may learn how to sense and respond to such changing road
conditions. He or she learns to become adaptive. Notice that
drivers can respond much faster and much better to conditions which they have learned
to adapt to than they do to conditions which they are learning about for
the first time.
Adaptation
refers to the driver’s ability to respond to current conditions.
Learning refers to the longer-term, cumulative process of building up a skill.
In formal terms, learning tries to adjust the control system so as to account
for parameters or structure in the plant which are initially unknown but
are not expected to change; this may include learning the dynamics or probability
distributions for changes in mass, friction, etc. -- thus, learning how to
adapt
to
changes in these specific parameters.
These
distinctions are of great importance, but they can become very fuzzy at times.
For example, the distinction between feedforward control and feedback control
depends on our making a distinction between “goal variable” sensors and other
sensors. This may not always be clear. Likewise, one may use a mathematical
design derived from a learning formulation, in order to build a
controller intended for use in adaptation. In fact, that approach has
been central to the modern field of “adaptive control.” (6,7).
Note that the four types of learning control discussed previously (cloning,
tracking, explicit optimization, implicit optimization) are all subcategories
of the learning control category here.
The
term “feedback control” is normally used in a very broad sense, including fixed
feedback control, adaptive control and learning control.
The
term “classical control” is used in very different ways, by different
researchers. Most often it refers to classical designs based on
The
term “robust control” has also been used in two different ways. In a broad
sense, “robust control” refers to the development of control designs which are
expected to remain stable, even if the parameters or states of the plant may be
different from what one expects initially. In a narrow sense, “robust control”
refers to specific techniques which have been developed to design fixed
feedback controllers which remain stable over a wide range of possible
values for the parameters of the plant. Some engineers prefer systems which are
robust in the narrow sense, because it can be difficult to analyze the
stability of systems with adaptive characteristics. However, there are many
cases where it is impossible to find a fixed controller powerful enough to
stabilize a plant over the entire normal operating range (17).
The
multistream approach described in the previous
section fits within the broad definition of robust control, but does not fit
within the narrow definition. It does not fit within the narrow definition
because it requires the use of a control structure general enough to permit
adaptive behavior. In other words, the controller must have some kind of
internal “memory” which implicitly keeps track of the road friction or mass or
other time-varying parameters of the plant. Much of the best research into
formal robust control also fails to meet the narrow definition, because it
includes the use of “observers” or “state estimators” which contain this kind
of memory (13). In other words, they are not fixed feedback controllers
as defined previously. Narendra has argued (6) that
traditional adaptive control may be thought of as a form of robust
control in the broader definition.
Stability, Performance,
Chaos and Verification
In
choosing between competing control designs, the engineer must usually trade off
three different criteria: (1) the actual degree of stability expected
from the system; (2) the actual degree of performance; (3) the degree of formal
confirmation available, to confirm that the system will always have the
expected degree of stability and performance, across different possible
conditions. In tracking problems, the issue of performance is often discussed
in terms of steady-state accuracy, transient response and disturbance rejection
(65). Stability is often discussed in terms of performance margins and the
acceptable range of uncertainty regarding the parameters of the plant to be
controlled.
The
distinction between actual stability and stability proofs is
especially important in many practical applications. As we climb up the ladder
of control designs, from static controllers up to nonlinear learning
controllers, the behavior of the controller becomes more and more complex. This
makes it more and more difficult to prove theorems about stability. However, if
learning control is used appropriately, the more complex designs make it possible
to achieve greater stability in a more robust way, over a wider range of
possible conditions.
In
a 1990 workshop (3), Narendra expressed this point in
a very graphic way. He described some simulations of an ordinary sort of
nonlinear tracking problem, which could be addressed by use of adaptive
control. First, he linearized the plant in the usual
fashion, and implemented the usual linear adaptive control designs for which he
and others had proven many, many stability theorems (6). Despite the theorems,
the controller blew up regularly in simulation. Then, he used a neural network
tracking design, which essentially just replaced a matrix with an ANN in an
ordinary adaptive control design. For that designs, he
could prove no theorems at that time, but the design remained stable across a
wide range of simulations.
Since
then, Narendra and others have in fact generated
dozens of theorems for various forms of “neural adaptive control” or tracking
control. But the lessons from this example still remain valid. The first lesson
is that many stability proofs make strong, simplifying assumptions about the
nature of the plant or of the environment. We can make stronger proofs by assuming
that the controller and the plant are both made up of independent linear
systems, but if the plant is not
actually linear, then the proofs become little more than empty window-dressing.
(There are other critical assumptions as well in these theorems.) The second
lesson is that we actually can develop proofs for more general controllers in
time, but it may take time. Prior to the development of formal stability
proofs, we must often start out by understanding the sources of instability in
a more practical sense, and developing those more stable designs which we later
prove theorems about. The third lesson is that the officials responsible for
verification and validation in different sectors may simply have no
absolute, valid mathematical guarantee available to them for any
kind of controller, in the real world.
The
practical development of verification and validation techniques is a complex
art, for which the needs vary greatly from application to application. For
example, many people claim that the control of manned aircraft must be one of
the strictest areas of application, where firm mathematical proofs of stability
are always essential, because of the safety issues with many human lives and
expensive vehicles at risk. However, with conventional aircraft, when there is
some sort of large unexpected damage -- such as a wing shot off, or a
hydraulics failure -- then the assumptions behind the proofs fly out the
window. For severe faults, the current control designs have almost a 100%
probability of failure -- of a fatal crash.
Back
in 1992, David White (3), working with Urnes of
McDonnell Douglas, developed a model-free reinforcement learning scheme which,
in simulation, could relearn the control of an F-15 in two seconds, in
half of the cases of severe damage. The McDonnell-Douglas simulation model of
the F-15 was a relatively realistic model, central to the development of that
vehicle. Thus simulations suggested that
the rate of crashes could be cut in half, by using a real-time learning scheme
in this application. 100% success was absolutely not required, because
it was impossible; simply to reduce the crashes from 100% to 50% would be a
great accomplishment. This has large implications both for aviation safety, and for the balance of power in aerial warfare.
Based
on the success of this early simulation work, the
Charles
Jorgensen of NASA Ames has reported that the first stage of neural-based
reconfigurable flight control has been totally successful. More precisely, it
has been used to land a full, manned MD-11 jumbo jet with all flight surfaces
locked up, to simulate a total loss of hydraulics. (See
http://ccf.asrc.nasa.gov/dx/basket/storiesetc/96_39.html.) The verification and
validation required for this experiment, involving collaboration between NASA
Ames and NASA Dryden, probably contains many lessons of general interest. (See
www.naga.gov for a discussion of the relkation
between these major components of NASA.) In general, the development of
practical techniques for verification and validation is similar in spirit to
the development of control software; it may be slow and laborious, but as time
goes on, it permits a gradual rise in the level of intelligence which can be
used in our control systems.
Strictly
speaking, the difference between seeking stability and seeking high performance
is not so great as one might imagine. For example, in multiperiod optimization, one can simply construct a
utility function (or cost function) which penalizes the system whenever it
enters certain forbidden zones. By minimizing the expected value of such a cost
function, one minimizes the probability of entering these zones. One maximizes
stability. Usually, when the random disturbances are Gaussian (which permits very
large disturbances on rare occasions), the probability of entering the danger
zone can never be reduced to zero. In that case, stochastic optimization may
indeed be the safest choice available, even though it does not permit zero
risk. For a truly realistic and complete description of the control problem,
one cannot really expect risk to equal zero, no matter what the control
strategy.
In
practice, users of optimization-based methods do not always choose a utility
function which only represents the concept of stability (i.e. minimizng risk). By adding terms to represent energy use,
pollution, jerkiness of motion, actuator constraints, and so on, one can
develop a controller based on a reasonable tradeoff between various aspects of
performance and stability, weighted according to the needs of the specific
application. Some users explore a variety of utility functionms,
in order to get a feeling for what the choices and trandeoffs
are.
The
optimization-based approach to stability may also open the door to a new
approach called “chaos control” (19). Leaders in the chaos field have argued
that traditional control too often focuses on trying to stabilize systems at a
fixed point, even when this is both expensive and unnecessary. By designing
highly sensitive plants which can even become chaotic, and by accepting
low-energy controls which only try to keep the plant within an acceptable region,
we may be able to save energy and increase performance. One might even argue
that the SR-71 aircraft already provides an example of this kind of tradeoff. The main difficulty with this idea of chaos
control lies in actually designing plants and controllers which embody the
idea. This difficulty could be overcome, simply by using learning control
systems based on multiperiod optimization (presumably
implicit optimization) with utility functions that keep the plant within an
acceptable region of operation. In fact, the use of such methods during the
design process would make it possible to tune the physical design
parameters, together with the control parameters, so as to maximize some
kind of combination of stability and performance together.
Once
we accept that real-world plants are in fact highly nonlinear, the most
rigorous, formal approach to achieving stability is fully nonlinear robust
control. (There also exists a far less general nonlinear theory, based on
feedback linearization.) The key results of this theory, mentioned previously,
are that the development of a robust control system is equivalent to the
solution of a differential game or of a stochastic optimization problem (13).
Thus, for example, Michael Athans of MIT, a major
leader of the mathematically rigorous group in aerospace control, has argued that
there is a critical need to develop general computer software to solve the
Hamilton-Jacobi-Bellman (HJB) equation for larger-scale, nonlinear systems in
order to implement this approach. The HJB equation is the foundation of multiperiod optimization (20), to be discussed in greater
detail towards the end of this article.
Unfortunately,
for all but the smallest systems, it is basically impossible to solve the HJB
equation exactly (except in a few very special cases, such as the linear
case.). Numerical methods or approximation methods are required. All solutions
of the HJB equation in such cases are in fact approximations, regardless
of whether they are called “numerical solutions” or “approximate solutions.” At
present, the safest procedure is to use the most accurate available
approximation methods, which include some of the implicit learning control
methods discussed here. In the long term, it will be crucial to develop more
formal tools to analyze the numerical approximation errors and their implications
for stability.
As
this encyclopedia goes to press, Richard Saeks of AAC
and Danil Prokhorov (66) of Ford Research
Laboratories have each reported new stabilities for
the MBAC designs discussed later in this article. Johan Suykens
of the Catholic University of Leuven (
Benefits and Costs of Using
Alternative Neural Networks
Once
we have decided to use a learning control design, when should we use neural
networks to provide the required subsystems? What kinds of artificial neural
networks (ANNs) should we use? Should we implement
learning in all of the subsystems?
In
many applications, the best strategy is to use a mix of ANNs
and other structures, at different stages of development. When the first stage
of controller development is based on some kind of physical plant model, for
example, it often makes sense to use that model directly, instead of taking the
time to train a neural network to approximate that model. On the other hand,
some learning control designs do not even require a model of the plant. Others
require the development of “dual subroutines” (9; 3, ch.10) which require some
effort to program and debug (21). In the future, when software becomes
available to generate these dual subroutines automatically, starting from
user-supplied models expressed in some standard format, it will become much
easier to use physical models directly.
Aside
from neural networks and first principles models, there are a host of methods
used in the past in engineering to approximate nonlinear functions --
gain-scheduling schemes,
In
summary, the practical choice is between using specialized nonlinear
structures, based on prior knowledge, such as a physical plant model, versus
the use of some kind of neural network to provide a general-purpose
ability to learn “any” nonlinear function. For maximum accuracy, one would want
to combine prior knowledge and learning-based knowledge (5); however,
this is not always worth the effort involved, and the best approach to
combining the two sets of information will depend on the particular
application. It will depend especially upon the accuracy and completeness of
the prior information, and on the availability of training data. Even after you
decide to use a neural network, the choice of which neural network to
use can often make or break your application.
In
the past (24), four general advantages have been cited for neural networks
here: universal approximation ability, ease of use, availability of chips and
PC boards, and links to the brain. (See also the article on Neural
Architectures.)
Almost
every major variety of ANN used in engineering has some variety of “universal
approximation” theorem attached to it, proving that it can approximate a smooth
function arbitrarily well, if given enough neurons. Andrew Barron (25)
has gone further, by proving that the most popular form of ANN -- the
multilayer perceptron (MLP) -- can approximate smooth functions of many
arguments with less additional complexity (i.e. fewer parameters) than are
required for “linear basis function approximators.”
Linear basis function approximators include most of
the common alternatives, such as the usual local networks and
These
results from Barron and Sontag confirm the existence of a very unpleasant
tradeoff, which has long been appreciated in intuitive terms by practical neurocontrol engineers. There is one class of ANN design --
the MLP and its extensions -- which can approximate functions in a parsimonious
way, and therefore do a better job of generalizing or extrapolating
from a limited amount of data. There is a different class of ANN designs
-- local designs like the Radial Basis Function (RBF) and the CMAC -- which permit very
rapid real-time learning and easier mathematical analysis. The present generation of off-the-shelf ANNs do
not provide the combination of good generalization ability and real-time
learning that the neurons of the brain provide! In the long term, advanced
research should make it possible to achieve more brain-like capabilities (28,
ch.13), and there are some practical tricks available (12, 23, 29, 3). For the
time being, however, this tradeoff between learning speed and generalization
ability tends to favor a greater use of offline learning than we would want in
the long term. In many practical applications, it is currently best to start
off with an approach based on offline learning, and then add elements of
real-time learning in a cautious, step-by-step manner.
Ease
of use has probably been the most dominant factor in the widespread use of ANNs in learning control. After all, if an ANN from off the
shelf can approximate a nonlinear function to any desired degree of
accuracy anyway, then why bother with all the complexity of representing the
function in other ways?
Availability
of special purpose chips and PC boards has also been a major factor. It was
crucial, for example, to the Ford (12) and AAC applications mentioned
previously. In ordinary computing or
supercomputing, one can normally fit only a small number of independent processors on a chip
(usually just one). This is because one must accommodate a large instruction
set, digital logic, and so on. However, for distributed ANN chips, it is good enough
to perform the same arithmetic operation over and over again in each processor.
Neural chips now on the market already contain up to thousands of
processors per chip. Computers based on such chips have demonstrated hundreds
of times more throughput per dollar, for what they do,
than conventional computers.
There
are many applications where traditional controllers have enough accuracy to do
the job, but are too large or expensive to implement. For example, one cannot
afford to put a large Cray into every airplane, car or manufacturing cell. In
such cases, neural network clones of the traditional controller can be
very useful. Many neural chip manufacturers also supply software subroutines to
simulate their chips, so that neurocontrol experts
can develop realistic designs which are easily migrated into hardware.
Naturally, the availability and throughput of chips is greater for some types
of ANN than for others.
Finally,
the link to the brain itself has also been a major motivation behind the
development and use of neural network designs. Because the brain itself is a neurocontroller(14),
it provides both an existence proof for the ultimate potential power of neurocontrol, and a source of clues for how to achieve that
power.
Model-Based Designs Versus Model-Free Designs
A
number of engineers have reported that neurocontrol
has worked better than classical control in their applications because it does
not depend on the quality of models available for the physical plant to be
controlled.
For
example, White and Sofge reported great success in
applying reinforcement learning to the continuous, low-cost manufacturing of
high quality carbon composite parts (3). Other approaches to this problem had
already been studied extensively by McDonnell-Douglas, because of the large
economic implications. A key reason why the earlier approaches did not work was
that the manufacturing process was so complex that the first-principles models
available were not very accurate. Unfortunately, after this technology had already
proven itself out in actual production, its commercialization was stalled by
contracting issues unrelated to the technology as such.
The
Air Force recently held
an in-depth workshop, inviting the lead engineers involved in
controlling high-powered optical instruments and associated space structures
(30). Those speakers reported, on the whole, that the use of modern control
theory had produced little if any improvement over classical control in these
applications, and had also been extremely expensive. The problem, they claimed,
was the need for very detailed, accurate plant models. On the other hand,
neural network tracking approaches -- particularly the work of David Hyland,
one of the experienced people in these applications -- had led to significant improvements,
at relatively low cost.
These
benefits have been quite real, but one must be careful to understand what they
really tell us. In actuality, the real choice is not between model-based
designs and model-free designs. The practical choice is between five
different alternatives, all quite common in neurocontrol:
(1) Truly model-free learning
designs, which include cloning designs, direct inverse tracking
designs, and smaller-scale reinforcement learning designs;
(2) Implicitly model-based
designs, such as the DRAL architecture discussed in the article on Neural
Networks for Feedback Control in this encyclopedia;
(3) Designs which require us to
train an ANN or some other learning-based system to predict or emulate the
plant;
(4) Designs which use expert
first-principles models of the usual sort;
(5) Designs which depend on “multistream models” -- stochastic descriptions of the plant
which include an expression of uncertainty about plant parameters, coupling,
and possible defects, in addition to random disturbances.
The
White and Sofge example was based on alternative
number one -- the use of a reinforcement learning system which pushed the
envelope on how large a task can be handled in a truly model-free design. The
Hyland system was based on alternative number three -- the use of a neural
model, which in turn depended critically on advanced prior work developing ways
to train neural models (31). (See (3, ch.10) for related theoretical
work.)
The
DRAL system, and some of the work by Berenji (32),
has exploited the assumption that there is a single action variable u(t), whose impact on the plant always has the same sign. It
is mathematically equivalent to the use of a model-based design in which
the model is simply x(t)=ku(t),
for some positive constant k. The stability and success of these systems helps
show how some of the neural model-based designs can in fact be very robust with
respect to the precise details of the model.
In
practical system development work, it is often critical to develop the best
possible initial controller based on prior information, before the
physical plant has actually been built. Even if real-time learning will be
used, this initial controller provides a starting point for further learning.
By definition, this initial controller must be based on some kind of
model, even if it is only a simulation model used to generate training data! At
this stage of development, true model-independence is impossible; the best one
can do is to reduce the degree of dependence by using a multistream
model instead of a conventional fixed, deterministic model. However, as
explained previously, success in training a controller to perform well on such multistream data requires the use of a controller capable
of “memory” or of “adaptive behavior.” Neural networks embodying “time-lagged
recurrence” (3,9,27) provide that capability.
It
has been argued that the brain itself relies heavily on large-scale
reinforcement learning designs which require the use of neural models (33).
Perhaps it may use hybrid designs, which make the results relatively robust
with respect to errors in those models; however, without exploiting some
knowledge about cause-and-effect relationships, and without an ability to form
expectations about the results of actions, the brain could never handle the
complexity of the decisions that it must make in everyday life.
Neurocontrol: Detailed Overview of the Designs
This
section will provide additional technical detail for the four broad classes of neurocontrol discussed previously -- cloning, tracking,
explicit multiperiod optimization and implicit multiperiod optimization. First, however, it will define
some notation and describe some common ANN subsystems which can be used when
building up a larger control system.
Notation
This
section will assume that the controller “sees” a vector X(t)
of m observables (X1(t),...,Xm(t))
at each time t, and that it will then output a vector u(t) of control
actions. In effect, X(t) represents the input
from the sensors, and u(t) the output to the actuators. Frequently there
will be an additional vector r(t) which
represents the estimated state of the plant. There may be a
reinforcement signal, U(t), or a utility function, U(X)
or U(r), which the control system tries to maximize over time. This
notation is slightly different from the traditional notation of control theory,
but it has a number of practical advantages related to the use of neural
networks and the links to other related disciplines. In mnemonic terms, the “X”
relates to “eXternal” data, the “r” to Representation
of Reality (usually through Recurrent neurons), and “U” represents utility.
Strictly speaking, the estimated state vector r(t)
is often composed of the combination of X(t) and R(t),
where R(t) represents the output of some (time-lagged) recurrent neurons
in one of the subsystems of the controller. In some designs it is assumed that
the plant to be controlled is “completely observable,” in which case X(t) and r(t) will be the same.
Common Subsystems
Most
ANN designs used in engineering can be built up in tinker-toy fashion by
linking together static neural networks. A static neural network
receives a vector of inputs X and generates a vector of outputs Y.
It contains an array of “weights” or parameters W. “Learning” usually involves
the adjustment of the weights, W, although it often involves some changes in
the connections in the network as well. The operation of a static neural
network can always be represented as:
![]()
where f is some function. To be precise, f is sometimes called
a vector-valued function of a vector, or simply a “mapping.”
When
we use designs that let us use any parametrized
static mapping, then of course we are not limited to neural networks as such.
When we actually use a static neural network, we may choose to insert
inputs from various different sources; therefore, the inputs and outputs will
usually be labeled as something else besides “X” and “Y.”
The
construction of larger systems by linking together static neural networks is
not just a useful mathematical fiction. It is also a useful approach to
building up models and flexible software to implement learning control. This
approach makes it easier to switch neural and nonneural
components in and out of a general learning design.
Learning
control designs are usually not built up directly from static neural
networks. They are built up from larger subsystems which in turn may be
made up of static neural networks or other parametrized
static mappings. The three most common types of subsystem today are: (1)
supervised learning systems (SLS); (2) systems trained on the basis of gradient
feedback; and (3) system identification subsystems.
Supervised
learning systems (SLS) try to learn the functional relationship between one
observed vector X(t) and another Y(t),
based on seeing examples of X(t) and Y(t).
For
real-time learning, we usually assume that the SLS starts out with an
initial set of weights W at each time t. Then, after it observes X(t), it makes a prediction for Y(t). Then,
after observing the actual value of Y(t),
it goes back and adjusts the weights W. In advanced research, this common
procedure is sometimes called “weight-based real-time learning.” There are
alternative approaches to real-time learning, still at the research stage,
called “memory-based learning” or “syncretism” (28, ch.13).
For
offline learning, we often assume that there is a database or training
set of examples, which may be labeled as X(t) and Y(t) for
t=1 to T. We often use the real-time learning approach, cycling through the
observations one by one, in multiple passes through the entire database. (These
passes are often called “epochs.”) Many SLS designs also provide an option for
“batch learning,” where the weights are adjusted only after some kind of
analysis of entire training set. In fact, most model estimation methods
taken from the field of statistics may be thought of as batch learning designs.
The
most common forms of SLS are based on some sort of error feedback, which may be
written:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() , (4)
, (4)
where “E” is some kind of error function. (See the articles on
Generalization and on Feedforward Neural Networks.) Equation 1 simply states
that the outputs of the neural network will be used as a prediction of Y(t). Equation 2 states that we calculate error as
some function of the actual value of Y(t) and
of the predictions. To measure error, most people simply use square error --
i.e., the
squared length of the difference between the two vectors; however, there are
some applications (especially in pattern classification) where other error
measures can work better. Finally, equations 3 and 4 are two equivalent ways of
expressing the same idea, using different notation. In both cases, we use the
derivatives (i.e., gradient vector) of error as a feedback signal, which will
then be used in training the ANN.
After
we know the derivatives of error with respect to the outputs of the ANN,
we can then go on to compute the derivatives of error with respect to the weights,
and then adjust the weights accordingly. The backpropagation algorithm, in its
original form from 1974 (9), permits us to calculate all the derivatives of
error with respect to the weights at low cost, for virtually any
nonlinear differentiable structure, not just ANNs!
Equations 1 through 4 are used most often with Multilayer Perceptrons. (See (9,
ch.8) for the most general form of MLP.) However, many other ANN learning
procedures can be expressed in this form as well.
In
supervised learning, the vector Y(t) is
sometimes called the vector of “desired outputs” or “desired responses” or
“targets.” Because this vector is known to us, we can use a variety of
nearest-neighbor prediction methods or associative memory designs, instead of
derivative-based learning. However, this only applies to subsystems which
perform supervised learning.
Sometimes,
as part of a control design, we need to adapt a static neural network f(X(t),W) without access to a vector of targets Y(t).
Typically, the larger design tells us how to calculate the vector F_Y(t), based on information elsewhere. Subsystems of
this sort must be trained on the basis of derivative feedback, which in
turn requires some use of backpropagation.
In
other words, for true supervised learning tasks, we have a choice between
derivative-based learning methods and other sorts of methods. For certain other
learning tasks, derivative-based learning is the only possible alternative.
Finally,
in control applications, we often need to use subsystems which learn to predict
the plant to be modeled. Conceptually, we might describe these systems as:
![]() (5)
(5)
where “t” represents physical time in the plant, assuming some kind of fixed
sampling rate for the sensors and actuators in the plant. Systems of this
general sort are called “neuroidentification”
systems. There is a ladder of designs available for neuroidentification,
similar to the ladder of designs in control.
In
the simplest neuroidentification designs, there is no
actual use of inputs before some fixed time interval k. The prediction problem
is actually treated as a supervised learning problem, with an expanded list of
inputs. Networks of this sort are called “Time Delay Neural Networks” (TDNN).
They are similar to “Finite Impulse Response” (FIR) systems in signal
processing, and to nonlinear autoregressive (NAR(k),
or, more precisely, NARX(k)) models in statistics (9,34). Unfortunately, these
models are often called “NARMA” models in the literature of adaptive control.
This usage has become so widespread in some areas that some people even
consider it a convention rather than an error; however, the original concept of
ARMA modeling is so important and fundamental in statistics (9,34) that the original usage should be preferred, even in
adaptive control theory. In statistics, “ARMA” refers to Mixed Autoregressive MOveing-Average models -- models which contain certain
common kinds of pattern in the random disturbance terms, patterns which AR
models cannot model in a parsimonious way; such patterns result whenever there
is “observation error,” error in sensing or measuring the state of the plant to
be controlled.
More
powerful designs for neuroidentification result from
adding one or both of two additional features: (1) time-lagged recurrence; (2)
dynamic robust training.
Time-lagged
recurrent networks (TLRNs) essentially contain a kind
of “internal memory” or “short-term memory,” as required for adaptive
behavior. They provide a generalization of true ARMA modeling capability,
which is also similar in spirit to Infinite Impulse Response (IIR) systems in
signal processing, and to Extended Kalman Filtering
(EKF) in conventional control. James Lo (35) has argued that TLRNs perform better than EKF in these applications. (The
reader should be warned, however, that there is another completely different
application of EKF methods in neurocontrol, involving
the acceleration of learning rates. For example, the Ford group has used
several generations of such acceleration methods(11,12).)
TLRNs are
harder to train than TDNNs; however, with an
effective use of the adaptive learning rate algorithm (3, ch.3) and appropriate
initial values, they can sometimes learn more quickly than TDNNs.
As
an example, the key successes of Ford Research in neurocontrol
depend very heavily on the use of TLRNs (11,12), trained by the use of backpropagation through time
(BTT). Likewise, the recent success of Jose Principe in speech recognition has
relied heavily on the various forms of TLRN he has used, also trained using
BTT. BTT was first implemented in 1974, on a classical multivariate ARMA
estimation problem (9); see (9,ch.8) for a more modern
tutorial, emphasizing the use of TLRNs. BTT is not
strictly speaking a real-time learning method, because it requires calculations
which operate backwards through time; however, it can be used in practice in a
real-time mode, in engineering applications which make use of fast electronic
hardware (11,12). Unfortunately, the most popular true real-time methods for
adapting TLRNs have severe disadvantages. See (27)
for a survey of these alternatives, including the new Error Critic design
which, in my view, is the only alternative which is plausible as a model of
what goes on in the brain.
Dynamic
robust estimation can be applied both to TDNNs
and to TLRNs, in order to improve the quality
of the resulting predictions. The key idea is to minimize errors in multiperiod prediction directly. This idea
has been used in various forms for a long time (9), but there is a substantial
need for more research to understand the deep theoretical principles involved,
and to develop designs which better reflect that understanding (3,ch.10). The
reader should be warned that “parallel identification” as used in adaptive
control is only the first step up this very high ladder (3), and often performs
worse than simple conventional training.
Finally,
in some applications, such as stock market trading, a simple predictive model
of the plant or environment may not be good enough. In some applications, it is
desirable to climb one step further up the ladder, to train true generalized
stochastic models of the plant or environment. Among the relevant tools are the
Stochastic Encoder/Decoder/Predictor (SEDP) (3,ch.13)
and, for smaller-scale problems, the Self-Organizing Map (SOM) (36). Here,
instead of trying to output the most likely prediction for Y(t), we try to build a kind of simulation model
for Y(t). We try to train a network which outputs possible values
for Y(t), in a stochastic way, such that probability of outputting any
particular value for Y(t) matches the true probability of that value
coming from the actual plant. (More precisely, it should match the conditional
probability of that value, given the information from times t-1, etc.) These designs have led to a few successful
implementations related to control, but there is a need for considerably more
research in this area. For example, no one has attempted to prove universal
stochastic process (probability) approximation theorems here analogous to the
theorems which Barron and Sontag have proven for the deterministic case.
Cloning
The
very first neurocontroller ever implemented was a
cloning controller developed by Bernard Widrow(37).
At
that time, no one used the words “neurocontrol” or
“cloning” in this sense. Even in the 1980’s, many
researchers thought of ANNs simply as supervised
learning systems, without allowing for other types of ANN design. In order to
develop a neurocontroller, they would follow two
steps: (1) build up a database of training examples of sensor
inputs X(t) and “correct control actions” u(t);
(2) use supervised learning to learn the mapping from X(t) to u(t).
At
first glance, this kind of exercise seems purely circular. If we already know
what the correct control actions are, for a wide variety of possible situations
X(t), then why bother to train a neural net?
Why not simply use the pre-existing controller or algorithm which tells
us what the correct control actions are? The answer is that the pre-existing
controller may actually be a special human being, or a very expensive computer
program, which may be too scarce, too expensive or too slow to use in all the
applications of interest. Therefore, this approach can be quite useful at times
as a way of ”cloning” the behavior of that
pre-existing controller.
It
is very unfortunate that many early papers using this approach did not
adequately explain where their database of “correct control actions” came from.
Even
within the area of cloning, we again face a ladder of designs. In all cases, we
begin by recording examples of X(t) and u(t)
from a human expert of pre-existing controller. In the simplest designs, we use
supervised learning to learn the mapping from X(t)
to u(t). In more sophisticated designs, we use neuroidentification
methods to predict the desired u(t) as a
function of X(t) and of earlier information. Whenever the human
expert or pre-existing controller need to have some kind of “memory” of earlier
time periods, as when they need to exhibit adaptive behavior, the sophisticated
designs should be used.
For
historical reasons, there is no really standard terminology in this area. In
the chemical industry, sophisticated cloning techniques are sometimes called
“operator modeling” (3,ch.10). In the robotics
industry, Hirzinger’s group has used cloning to copy
specific skilled movements of human operators, and called this “skill
learning.” (Hirzinger’s group is perhaps the most
advanced group in the world today applying a broad spectrum of learning-based
intelligent controllers to practical real-world applications, including space
robots, flexible high-throughput manufacturing robots, medical robots, and
others(38).) The neural aerospace company mentioned previously (AAC) has
actually occasionally used the word “cloning.”
Some
roboticists may ask what the connection is between
cloning as described here, and the older pendant-based methods of training
robots. Very simply, the older methods yield a static controller, as previously
defined, while the cloning methods yield an ability to respond to sensor inputs
X; in other words, they can be used to train feedforward, feedback or
even adaptive controllers.
In
many applications, cloning approaches are a good place to start, even if the
ultimate goal is to develop an optimizing controller. For example, even
before developing any automatic controller, one may try to develop a telerobotic interface, to permit a human being to directly
control a robot designed for the application. If the human cannot learn to
control this robot, one may reconsider the physical robot design. If the human
can control it, one can then clone the human behavior, and use the result as
the starting point for a more sophisticated learning controller.
Tracking
Tracking controllers are defined as
controllers which try to make the plant stay at a desired setpoint,
or follow (track) a desired trajectory over time. More precisely, the control
actions u(t) are chosen so as to make the actual observed state X(t)
match a desired reference trajectory, X*(t) or Xr(t),
supplied by the user. (The setpoint case, also called
“homeostatic control,” is the case where the desired states X*(t) do not
change over time -- except when the user changes the setpoint.).
Both
in neurocontrol and in classical control, the
majority of academic papers published today focus on tracking control. As a
result, the literature is extremely complex and somewhat difficult to summarize
accurately. Many neural tracking designs are essentially just conventional
tracking designs, or adaptive control designs (6,7),
with matrices replaced by neural networks. Unfortunately, many researchers have
made the mistake of assuming that tracking problems are the only
problems of interest to control theory.
Roughly
speaking, there is once again a ladder of learning-based designs available:
(1) Direct inverse control;
(2) Model-based or indirect adaptive
control, based on the short-term minimization of a simple general-purpose
measure of tracking error (usually just square error);
(3) Model-based or indirect adaptive
control in the short-term minimization of a
special purpose, application-specific Liapunov
function;
(4) Hybrid designs, which combine
one or more of the previous three, together with
the
use of a pre-existing fixed feedback controller;
(5) Designs which convert the
tracking problem into a task in multiperiod
optimization.
As
discussed previously, the “models” required in these designs are sometimes
replaced by simple implicit relations like y=kx,
where k is a positive scalar. The term “direct” is sometimes used to describe implicitly
model-based designs of this sort.
True
direct inverse control (DIC) was once the most popular form of neurocontrol. DIC was applied most often to robot control
(1,39), or to biological models of hand and eye
movements (39,40). In DIC, we usually assume that there is a simple relation
between the control variables and the position of the robot arm, which can be
expressed as X=g(u). For example,
if u consists of three variables, each controlling the angle of one of
the three joints in a robot arm, then g is the function which determines
where the hand will be located in spatial coordinates. If the
function g happens to be invertible, then there will be a unique solution
for u, for any vector X:
![]() (6)
(6)
In
DIC, one tries to learn the function g-1, simply by
observing pairs of u(t) and X(t) and
using supervised learning. Then, to control the arm, one simply sets:
![]() (7)
(7)
When
the mapping from X to u is learned in this simple static way
(39), the errors tend to be about 3% -- too large for realistic robotic
applications. However, when the neural network is also given inputs from past
times, very accurate tracking becomes possible (1,40).
Miller has shown videos of a system based on this approach which could learn to
push an unstable cart around a figure 8 track with very highly accuracy, and
then readapt (with real-time learning) within three loops around the
track after a sudden change in the mass on the cart. Miller also developed a
VLSI control board for use in a conventional robot, but the
DIC
does require the assumption that the function g be invertible. If the
vector u has more degrees of freedom than the vector X, then this
is clearly impossible. Some ANNs have been developed
which effectively throw away the extra degrees of freedom in u. But most
control engineers have moved on to model-based designs, which are usually
considered to be more powerful and more general, and which permit a systematic
exploitation of the extra control power of any extra degrees of freedom. (See (6) for a discussion of direct versus indirect adaptive
control.)
Model-based
adaptive control is the dominant form of neurocontrol
today in academic publications. The papers by Narendra
and coauthors, starting from (41), have played a leading role in this
development. (See also his papers in (1,3,8).) A wide
variety of designs have been considered, a wide variety of theorems proven, and
a wide variety of simulations studied. There have certainly been some
real-world applications as well. But again, it is difficult to summarize the
literature accurately in a brief overview. In this overview, I will assume a
conventional sampled-time approach. (Narendra usually
uses a differential equation formulation, which is more or less equivalent.) Neurocontrollers of this sort had already been implemented
by 1987, by Jordan and Rumelhart and by Psaltis et al (42), but the later more rigorous analysis
has been crucial to the use of these methods.
On
the whole, most of these designs effectively involve the effort to minimize
tracking error at time t+1, the very next time period:
![]() (8)
(8)
(Narendra uses the letter “e” instead of “U”. The letter U
emphasizes the link to optimization methods, and reminds us that this “error”
is actually a kind of physical cost rather than something like a prediction error.)
These designs require the use of an Action network and a Model network, both of
which can be adapted in real time. The Model network learns to predict X(t+1) as a function of X(t) and u(t)
(and perhaps of earlier information);
it
is adapted by neuroidentification methods. The Action
network inputs X(t) (and earlier information)
and outputs u(t). The Action network is trained on the basis of derivative
feedback, which may be calculated as follows:
![]() (9)
(9)
In
actuality, this calculation may be performed more economically by “backpropagating through” the Model network; in other words,
one may use the “dual subroutine” for the Model network, in order to reduce the
computational costs. (9, ch.8; 3, ch.10). In order to
insure stability, it is important to limit the overall speed of learning in
these networks.
Numerous
general stability theorems have been proven for this class of design, very
similar to the theorems which exist for adaptive control in general.
Nevertheless, all of these theorems (both neural and classical) do require some
very stringent conditions. In some applications, like certain forms of
vibration control, one may expect certain instabilities to be damped out
automatically, so that these stringent conditions will be met. Great success
has been reported in some applications (30). But in many application domains --
like chemical plants and aerospace vehicles -- there are major barriers to the
use of any standard adaptive control techniques, neural or classical,
because of some bad historical experience with instabilities.
There
are many plants where actions which appear stabilizing in the short-term
(at time t+1) will have the opposite effect in the long-term. Consider,
for example, the bioreactor benchmark problem in (1). Lyle Ungar
has shown how all kinds of neural and classical adaptive control designs still
tend to go unstable when used on that simulated plant. However, when engineers
have used multiperiod optimization designs
(which account for long-term effects), they have had great success in
controlling that plant (43).
In
ordinary control engineering, there are actually two standard ways to overcome
these potential instabilities. One is to treat the tracking problem as a multiperiod optimization problem. The other is to replace
the function U in equations 8 and 9 by an application-specific Liapunov function, which meets some other stringent
requirements, related to the dynamics of the plant, which must be known. For
certain application-specific areas of nonlinear control, such as stiff robot
arms, this has been a very useful approach. Unfortunately, it places great
demands on human ingenuity to find the Liapunov
functions which meet all the requirements, in any complex application. The need
to use a simple pre-ordained model of the plant will tend to force the use of a
restrictive class of physical plants, as in robotics. Hirzinger’s
group (38) has shown that substantial improvements in performance are possible,
if one explores a wider class of physical plants (like light-weight flexible
arms), which then require a more powerful control design.
In
any event, neural learning designs need not be an alternative to Liapunov-based adaptive control. Instead, the “Critic”
networks in some reinforcement learning designs (to be described below) may be
used as a constructive technique to actually find the Liapunov functions for difficult, complex applications
(44). In fact, many of the special-purpose Liapunov
functions used in practice actually came from an analytical solution of
a multiperiod optimization problem. (See for example
the work of Sanner at the
The
hybrid neural/classical
designs mentioned above are largely beyond the scope of this
article. Particularly interesting examples are some of the methods described by
Frank Lewis elsewhere in this encyclopedia, the Feedback Error Learning design
of Kawato et al (1), and the “Seraji-like
Neural Adaptive Controller” as described by Richard Saeks
of AAC at many conferences. All of these designs use the traditional feedback
controller to insure stability even before learning begins, but also exploit
real-time learning in order to improve performance or stability over time.
Finally,
to convert a tracking problem into a multiperiod
optimization problem, one need only minimize U (as defined in equation 8) over
future time periods. In principle, one tries to pick u(t)
so as to minimize (or maximize):
![]() (10)
(10)
In
practice, one can then add additional terms to the utility (or cost) function,
so as to minimize some combination of tracking error, energy consumption,
jerkiness, depreciation, etc. This class of designs has very strong stability
properties. For example, Model-Predictive Control (MPC), a method in this
class, has received wide acceptance in the chemical industry, where
conventional forms of adaptive control are usually considered too unstable to
be trusted.
Explicit Multiperiod Optimization
Until
recently, explicit multiperiod optimization was the
method of choice for very difficult, realistic challenges in neurocontrol. Because the method is very straightforward
and exact, it still deserves a place in virtually every serious toolbox for neurocontrol.
In
the simplest version of the method, the user must supply a deterministic Model
of the plant to be controlled (a Model which could be based on neuroidentification) and a utility function U(X).
The goal is to train an Action network, which inputs X(t)
and outputs u(t), so as to maximize (or minimize) the sum of U over
time.
In
each iteration, we start out at time t=1. We use the Model network and the initial
version of the Action network to generate a stream of predictions for X(t) from time t=1 up to some final time t=T. We then
use backpropagation through time (BTT) to calculate the complete
gradient of Utotal with respect to the
weights in the Action network. (Utotal is
just the sum of U(t) from t=1 to t=T.) We adjust the
weights in response to that gradient, and then start a new iteration or quit.
This
is more or less equivalent to the classical multiperiod
optimization methods called the calculus of variations (20) and differential
dynamic programming (45). The main novelty is that BTT allows a faster
calculation of derivatives, and the use of neural networks allows a general
function approximation capability. Complete pseudocode
for the approach may be found in (9, ch.8).
This
simple version was used in Widrow’s classic truck
backer-upper (1) and
A
slight variant of this approach is to adapt a schedule of actions from
time t=1 to t=T, instead of an Action network. That approach
was used in the official DOE/EIA model of the natural gas industry, which I
developed circa 1986 (21). It was also used in the “cascade phase two”
design for robot arm control by Uno, Kawato et al (1), and in the chemical plant controller of McAvoy et al (3,ch.10).
Instead
of simply minimizing or maximizing Utotal
in an unconstrained manner, one sometimes needs to minimize it subject to
constraints. In that case, we can combine the approach described previously
with more classical methods designed to combine gradient information and
constraint information, to arrive at a schedule of actions. In fact, the work
of McAvoy et al takes this approach, which may be
seen as a useful special case of a more conventional control method, nonlinear
Model-Predictive Control.
In
the robotics area, Hirzinger has also applied
a variant of these approaches very successfully in his “outer loop
optimization” (38). Hrycej of Daimler-Benz has also
reported a number of successful applications (48).
Note
that all of this work assumes that a Model of the plant is available, and
proceeds as if the Model were perfectly exact. One could account for random
disturbances or errors, in principle, by using the methods of Differential
Dynamic Programming (45). However, there is reason to question the efficiency
of these methods in accounting for such effects, relative to the implicit
optimization methods described in the next section.
There
are other ways to perform explicit multiperiod
optimization, without using BTT. Some of these methods involve less accurate
methods of computing gradients, or more expensive ways of computing the same
derivatives (27). Others are totally derivative-free methods, like evolutionary
computing (EC), which includes genetic algorithms (GAs)
as one special case. EC works by simulating entire populations of possible
control designs, and selecting out those with the best overall observed
performance. EC can be very useful for small enough control problems, in
off-line learning, and can also be used to provide initial values for a
gradient-based system. (See the work of Tariq Samad of Honeywell (70) and of Krishnakumar
(71) for some practical control work using EC.) They can provide an alternative
to step-by-step learning, in avoiding local minimum problems. In the long-term,
however, a brain-like approach would have to involve a totally different sort
of stochastic search method for real-time learning, in order to enable the
solution of larger problems (64,68).
Disadvantages
of the explicit approach relative to the implicit approach are: (1) the
assumption that the Model is exact; (2) the inability to account for payoffs or
costs beyond time T, in the receding horizon approach; (3) the computational
cost of simulating T time periods in every cycle of adaptation. It is possible
to eliminate the second disadvantage, by using a hybrid design, in which
a Critic network supplies the derivatives which start up the gradient
calculations for t=T (15).
Implicit Multiperiod Optimization
This
class of designs if the most complex, sophisticated and brain-like class of
designs in neurocontrol. They learn to maximize the
sum of future utility without ever developing an explicit schedule or
plan for what will happen in the future. In effect, they can solve problems in
“planning” without an explicit plan.
More
concretely, these designs try to maximize the sum of future utility, in
situations where there does not exist an exact, deterministic model of the
plant or environment. There may exist a stochastic
model, which can be used to simulate the environment, but not a
deterministic model. In formal terms, these are learning designs which try to
solve general problems in nonlinear stochastic optimization over time. Of
course, these methods can also be used in the special case where the
environment does happen to be deterministic.
In
control theory, there is only one family of algorithms which can find the exact
solution to such problems, in a computationally efficient manner: dynamic
programming. Designs which learn to approximate or converge
to the dynamic programming solution are sometimes called “approximate
dynamic programming” (ADP)(3) or “neurodynamic
programming” (49). As an alternative, these designs are sometimes called
“reinforcement learning” designs. (The connections between
reinforcement learning, approximate dynamic programming, backwards feedback and
neural networks were first discussed -- albeit in very crude form -- in
1968(50).) The most precise label for these designs, favored by experts
in this field in their most technical discussions, is the term “adaptive
critic.” The phrase “adaptive critic” was coined by Bernard Widrow,
who implemented the first working neurocontroller in
this class(51). This is the most precise label because
there are other ways to approximate dynamic programming which do not involve
learning, because the designs in this class do not always require neural
networks, and because the term “reinforcement learning” has been used in the
past to refer to a very wide range of concepts beyond the scope of this
encyclopedia.
In
dynamic programming, the user normally supplies a utility function U(X,u), and a
stochastic model of the environment, which may be written:
![]() , (11)
, (11)
where Wf represents the parameters or
weights of the model and e(t) is a vector of random numbers representing
random disturbances. The problem is to find a strategy of action, u(X),
so as to maximize:
![]() (12)
(12)
where r is a user-supplied parameter corresponding exactly to the idea of an
“interest rate” or “discount factor” in economics, and where the angle brackets
denote the expectation value of this sum. In many applications, T is
chosen to be infinity or r is chosen to be zero or both. In some papers, the
term 1/(1+r) is called “g.” U(X,u) often depends only on X; however, I
include u here for the sake of generality.
In
dynamic programming, one solves this problem by solving the Bellman
equation, which may be written as:
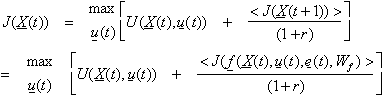 (13)
(13)
Solving the Bellman equation means finding the function J(X)
which satisfies this equation.
After
we have found that function, we simply pick u(t)
at all times so as to maximize the right-hand side of this equation. After we
know J(X), the selection of u is a problem in short-term maximization.
In other words, dynamic programming converts a difficult problem in long-term
maximization or planning into a more straightforward problem in short-term
maximization.
In
theory, dynamic programming could be used to solve all problems in
planning and control, exactly. In practice, the sheer computational cost
of solving the Bellman equation becomes prohibitive even for many very small
control problems. The cost rises exponentially with the number of variables in
the plant or environment. Plants governed by a single state variable are
usually manageable, but
plants based on ten are usually far too complex.
Adaptive
critic designs approximate dynamic programming, by learning an approximation
to the function J(X) (or to its gradient or to something very similar.).
The neural network (or other approximator) which
approximates the J function (or gradient...) is called a “Critic.” An “adaptive
critic” system is defined as a control system which contains a Critic network,
adapted over time through some kind of generalized learning procedure.
The
adaptive critic family of designs is extremely large and extremely diverse. It
includes some very simple designs, like the Critic/Actor lookup-table system of
Barto, Sutton and Anderson (BSA)(52),
which has become extremely popular in computer science. As an example, an
advanced version of this system has been used to play backgammon. It has
achieved master class performance in that game, proving that adaptive critic
designs can in fact achieve something like real “intelligence.” (53). The
adaptive critic family also includes more complex, more “brain-like” designs (3,33,54,55,56), combining a Critic network, an Action network
and a Model network. These more complex designs have demonstrated the ability
to handle a variety of difficult test problems in engineering, more effectively
than alternative designs, both neural and nonneural.
The family also includes a special form of “Error Critic” first proposed in
order to explain certain features of the cerebellum (3,ch.13).
This form of critic has apparently been extremely successful in some practical
but proprietary applications in the automotive sector. Finally, the adaptive
critic family also includes “two brain” and “three brain” designs which, in my
view, should be rich enough and powerful to capture the essence of the
higher-level intelligence which exists in the brains of mammals (14,57).
Space
does not permit a complete description of these four subfamilies in this
article. However, a few general observations may be of use to the reader, to
supplement the citations mentioned above.
In
the Barto-style family of methods, the most popular
methods are the original BSA design (52) and Q-learning of Watkins (58). In the
BSA design, the Critic learns to approximate the function J(X). Thus the
Critic inputs a vector of observed sensor data X, and outputs a scalar
estimate of J. The Critic is trained by a “temporal difference method,” which
is a special case of Heuristic Dynamic Programming (HDP) (59), first published
by the author in 1977.
In
HDP, one trains the Critic by use of supervised learning. At each time t, the
input vector is simply X(t). The target
“vector” is the scalar U(t)+(J(t+1)/(1+r)), the
right-hand side of the Bellman equation, using the Critic itself to estimate
J(t+1). There are two counterintuitive aspects to this design: (1) the training
for time t cannot be carried out until after the data for t+1 are known (or
simulated); (2) the weights in the Critic are adapted as if the target is
constant, even though we know that a change in those weights would change the
estimate of J(t+1)! Many researchers have responded to
the second aspect by reinventing a “new” method, which adjusts the weights WJ
so as to minimize:
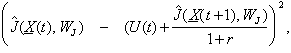 (14)
(14)
where WJ are the weights in the Critic network, and J-hat refers
to the Critic network. Unfortunately, this sensible-looking procedure leads to
incorrect results almost always, at least in the linear-quadratic case (59).
HDP proper always converges to the correct results in that case.
The
Barto-style family can sometimes be very robust and
very efficient, when the action vector u(t)
actually consists of a small number of discrete choices. When the action
variables are truly continuous, or when there are many action variables, the methods
are still robust, but extremely slow to converge. Furthermore, the validity of
these designs requires the assumption that X(t)=r(t),
i.e. that the plant being controlled is completely observable. In practice, we
can overcome that limitation by estimating the state vector r(t), and providing the entire state vector as input
to the Critic; however, the estimation of the state vector tends to require
something like a neuroidentification component.
As
we climb up the ladder of designs, the next method beyond the Barto-style methods is “ADAC” -- the Action-Dependent
Adaptive Critic, closely related to Q-learning, and developed independently in
1989 (3). (In fact, many authors have reinvented ADAC and called it “a new
method for modified Q-learning.”) This design was applied successfully by
McDonnell-Douglas in several real-world problems, including the manufacture of
high-quality carbon-carbon composite parts and simulated control of damaged
F-15s (3). ADAC can handle larger problems than the Barto-style
family, but it still has limits on scale, and problems related to “persistence
of excitation.” In a strict sense, there are actually three designs in the ADAC
group; the McDonnell-Douglas work used the simplest of the three, which is
called Action-Dependent HDP (ADHDP).
Next
up the ladder are several designs which have been called “Model-Based Adaptive
Critics” (MBAC) or “Brain-Like Intelligent Control” (33,54,55,56).
These designs all require the use of three core components, a Critic,
and Action network, and a Model. In the simplest design, the Critic is again
trained by HDP. (Some authors now use the term “HDP” to refer to this entire
design.) The Model is typically trained by some sort of neuroidentification
procedure. The Action network is trained based on the derivatives of J(t+1) with respect to the weights in the Action network;
these derivatives are calculated by backpropagating
through the Critic, the Model and the Action network, in that order. (See (3)
and (9,ch.8) for critical implementation details.) The
Model plays a crucial role here, in distributing the feedback from the Critic
to specific Action variables; this kind of rational distribution or
“credit assignment” allows these designs to handle larger-scale problems than
the simple two-network designs can. This subfamily also contains two more
advanced designs, Dual Heuristic Programming (DHP) and Globalized
DHP (GDHP), proposed before 1981 (9,ch.7), and their
action-dependent variants. These more advanced designs use the Model in
training the Critic itself, so as to improve credit assignment still further.
Research in neuroscience has shown that certain parts of the brain do indeed
seem to “learn to predict” as a Model network would (14). Grossberg
has pointed out many times that a large part of the results from animal
learning experiments require the existence of an “expectations” system in the
brain. In fornal terms, DHP is a learning-based
approximation to the stochastic generalization of the classical Pontryagin principle as given in (3, ch.13). Some
additional recent implementations are cited in (64) See also (69).
Unfortunately,
the term “model-based reinforcement learning” has sometimes been broadened to
include designs of the Barto subfamily. In true,
full-fledged brain-like systems, one would expect a Model network to be used to
perform at least three functions: (1) the credit assignment function,
discussed in the previous paragraph; (2) the estimation of the state vector r(t) to be input to the Critic and Action network;
(3) simulations or “dreams” (60, 1 ch. 8) of possible
future r(t), for use in training the Critic and Action network. Only the
first function really changes the core design of the adaptive critic proper;
the others simply alter the flow of inputs into that core.
Finally,
some new designs have recently begun to emerge in theory
which try to bridge the gap between “brain-like” designs and the major
features of higher-order intelligence in the mammalian brain. The GDHP design
(60) does actually meet certain basic tests (33) which a credible, first-order
model of intelligence in the brain should meet. However, if the “sockets” in
that design are filled in with conventional feedforward or Hebbian
neural networks, the system is unable to learn to solve certain basic problems in
spatial navigation (26,27) which a truly brain-like
system should be able to handle. This difficulty cold be solved fairly easily,
in principle, by coupling together two entire “brains” (adaptive critic
systems) in one design -- a higher-order “master” system built out of SRN
networks (26,27) and a fast low-order “slave” system based on feedforward
networks (14). However, there is still a need for a kind of “middle brain” as
well, in order to explain phenomena such as task learning, temporal chunking, spatial
chunking, the basal ganglia, and so on. The pathway to developing such neurocontrollers now seems fairly clear, but considerable
research remains to be done (14, 57). Furthermore, many researchers would argue
that there exists another gap, between the intelligence one observes in the
ordinary mammalian brain and the higher-order intelligence or consciousness in
the human mind (61, 9 ch. 10); however, one may still
expect that an understanding of the former should contribute to a greater
possibility of understanding the latter. Difficult testbed
problems in engineering and computer science will play a crucial role in
permitting the development of mathematical concepts necessary to both sorts of
understanding.
Bibliography
1. W.T.Miller, R.Sutton & P.Werbos (eds),
Neural Networks for Control, MIT
Press, 1990, now in paper. Warning: pseudo in ch.2. contains
errors; see (3,15).
Also, the discussion of recurrent
networks is somewhat dated.
2. N.Wiener, Cybernetics,
or Control and Communications in the Animal and the Machine,
2nd., ed.,
MIT Press, 1961.
3. D.White & D.Sofge, eds,
Handbook of Intelligent Control, Van Nostrand, 1992.
4. P.Werbos, The cytoskeleton: Why it may be crucial to human
learning and to neurocontrol,
Nanobiology,
Vol. 1, No.1, 1992.
5. P.Werbos, Econometric techniques: theory versus practice, Energy, Vol. 15, No. 3/4 March/April 1990.
6. K.Narendra and A.Annaswamy, Stable Adaptive Systems,
7. K.J.Astrom & B.Wittenmark, Adaptive Control,
8. M.M.Gupta & N.K.Sinha, eds, Intelligent Control Systems, IEEE Press, 1996.
9. P.Werbos, The Roots
of Backpropagation: From Ordered Derivatives to Neural Networks and Political Forecasting, Wiley, 1994.
10.
P.Werbos, Neurocontrol in
A. Maren (ed),
Handbook of Neural Computing
Applications, Academic, 1990.
11 L.Feldkamp, Puskorius,
12 G.V.Puskorius, L.A.Feldkamp &
L.I.Davis, Dynamic neural network methods applied to on-vehicle
idle speed control, Proc. Int’l Conf. Neural Networks: Plenary, Panel and Special Sessions, IEEE, 1996.
13.
J.S.Baras and N.S.Patel,
Information state for robust control of set-valued discrete time systems, Proc. 34th Conf. Decision and Control (CDC),
IEEE, 1995. p.2302.
14. P.Werbos, Learning in the brain: An engineering
interpretation. In K.Pribram, ed., Learning as Self-Organization , Erlbaum 1996.
15. P.Werbos, Optimization
methods for brain-like intelligent control, Proc.
IEEE Conf. CDC, IEEE, 1995. Also see (33).
16 R.M.Pap, Design of neurocontroller
to operate active flight surfaces, Technical report
to NSF
grant ECS-9147774.
17 G.Sachs, W.Schroder,
M.Heller &P.Sacher,
Robust control concept for a hypersonic test vehicle, AIAA-95-6061,
18.
M.L.Padgett & T. Lindblad,
eds, Virtual
Intelligence , SPIE Proceedings Series Volume 2878, SPIE - The
International Society for Optical Engineering, Bellingham,
19.
I.Peterson, Ribbon of chaos, Science News, Vol.139, No.4, Jan. 26, 1991.
20 A.Bryson & Y.C.Ho,
Applied Optimal Control, Ginn, 1969.
21 P.Werbos, Maximizing
long-term gas industry profits in two minutes in Lotus using neural network
methods, IEEE Trans. SMC, March/April
1989.
22 R.A.Jacobs, M.I.Jordan,
S.J.Nowlan & G.E.Hinton,
Adaptive mixtures of local experts, Neural
Computation, Vol. 3, p.79-87.
23 T.W.Long, A learning controller for
decentralized nonlinear systems, American
Control Conf., IEEE, 1993.
24 E.Fiesler & R.Beale, eds, Handbook of Neural Computation,
25 A.R.Barron, Universal approximation bounds for superpositions of a sigmoidal
function IEEE Trans. Info. Theory 39(3) 930-945, 1993.
26 P.Werbos & X.Z.Pang, Generalized maze navigation: SRN critics solve
what feedforward or Hebbian nets cannot.Proc. Conf. Systems, Man and Cybernetics (SMC) (
IEEE, 1996. (An earlier version appeared in WCNN96 and Yale96[57].)
27 X.Z.Pang & P.Werbos, Neural network design for J function
approximation in dynamic programming, Math.
Modelling
and Scientific Computing (a Principia Scientia journal),
Vol. 5, NO.2/3, 1996 (physically 1998). Available also as adap-org 9806001 from xxx.lanl.gov/form, using the “Other
Groups” field set to “nlin-sys.”
28.
V. Roychowdhury, K.Siu and A.Orlitsky (eds),
Theoretical Advances in Neural Computation
and Learning, Kluwer, 1994
29 J.T.Lo, Adaptive system identification by nonadaptively trained neural networks, Proc. Int. Conf. Neural Networks, IEEE, 1996, p.2066-2071.
30.
M.Obal and A. Das, Proceedings of a Workshop on
Neural Decision and Control_Technology for Aerospace Systems.
(February 1997). Phillips Laboratory (AFMC), Kirtland
Air Force Base,
31. Neural
Network System Identification : Final Report,
Contract NAS1-18225 Task 9,
for NASA Langley, Harrris Corp. Gov’t Aerospace Sys. Div.,
32. H.Berenji, A
reinforcement learning-based algorithm for fuzzy logic control, Int’l J. Approx. Reasoning, Vol.6, No.2,
February 1992.
33. P.Werbos, Optimal neurocontrol:
Practical benefits, new results and biological evidence, Proc. World Cong. on Neural Networks(WCNN95),Erlbaum,
1995. This and several
other papers cited here may be obtained from links on www.eng.nsf.gov/ecs/werbos.htm
34.
G.E.P. Box & G.M.Jenkins, Time-Series Analysis: Forecasting and Control,
35.
J.T.Lo, Synthetic approach to optimal filtering. IEEE Trans. Neural Networks,
Vol. 5, p.803-811, September 1994. See also J.T.Lo,
Adaptive optimal filtering by pretrained neural networks, Proc. World Congress on Neural Networks, Erlbaum, 1995, p.611- 615.
36.
T.Kohonen, The self-organizing map, Proc. IEEE, Vol. 78, No.9, Sept. 1990.
See also a more recent book by which elaborates on the issue of probability
densities:
H.Ritter, T.Martinez
and K.Schulten, Neural
Computation and Self-Organizing Maps, Addison-Wesley,
1992.
37.
B.Widrow & F.W.Smith,
Pattern-recognizing control systems, Computer
and Info. Sci. (COINS) Proc., Spartan, 1964.
38.
G.Hirzinger, R.Koeppe, A.Baader,F.Lange,E.Ralli,A.Albu-Schaffer,R.Staudte
& G.Wei,
Neural Perception and manipulation
in robotics, in M. van der Meer & R.Schmidt, eds,
Kunstliche Intellkigenz, Neuroinformatik und Intelligente Systeme,
DLR,
39 M.Kuperstein, INFANT neural controller for adaptive sensory-motor
coordination, Neural Networks, Vol.
4, No.2, 1991
40 P.Gaudiano & S.Grossberg,
Vector associative maps: Unsupervised real-time error-based learning and
control of movement trajectories, Neural
Networks, Vol. 4, p.147-183, 1991.
41 K.S.Narendra and K.Parasarathy,
Identification and control of dynamical systems using neural networks, IEEE Trans. Neural Networks, Vol. 1,
No.1, p.4-27, March 1990.
42 D.Psaltis,A.Sideris and A.Tamamura, Neural controllers, in Proc. Int..Conf. Neural Networks, IEEE, 1987,
p.IV-551-558.
43 F.Yuan, L.Feldkamp,
G.Puskorius & L.Davis,
A simple solution to the bioreactor benchmark problem by application of
Q-learning, Proc. World Congress on
Neural Networks, Erlbaum, 1995.
44. P.Werbos, New methods for the automatic construction of Liapunov functions. In K.Pribram, ed., Origins:
Brain and Self-Organization, Erlbaum, 1994, p.46-52.
45 D.Jacobson
& D.Mayne, Differential
Dynamic Programming, American Elsevier, 1970.
46 M.Jordan, Generic constraints on
underspecified target trajectories. In Proc.
IJCNN,
IEEE, June 1989.
47
T.W. Long, Final Report to NASA Langley,
48 T.Hrycej, Model-based training
method for neural controllers. In Aleksander I and Taylor
J eds Artificial Neural Networks 2.
49 D.P.Bertsekas & J.N.Tsiskilis,
Neuro-dynamic Programming,
50 P.Werbos, The elements of
intelligence. Cybernetica (
51 B.Widrow, N.Gupta
& S.Maitra, Punish/reward: learning with a Critic
in adaptive threshold systems, IEEE
Trans. SMC, 1973, Vol. 5, p.455-465.
52 A.Barto, R.Sutton and C.Anderson, Neuronlike adaptive
elements that can solve difficult learning control problems, IEEE Trans. SMC, Vol. 13, No.5, 1983,
p.834-846.
53 G.J.Tesauro, Practical issues in
temporal difference learning. Machine
Learning, 1992, 8:p.257-277..
54 D.Prokhorov & D. Wunsch,
Adaptive critic designs, IEEE Trans.
Neural Networks, Vol. 8, No. 5, p.997-1007, 1997.
55 P.Eaton, D.Prokhorov & D.Wunsch, Neurocontrollers for
ball-and-beam system, in Proc. Artificial
Neural Networks in Eng. (ANNIE), ASME Press, 1996.
56 N.Visnevski & D.Prokhorov,
Control of a nonlinear multivariable system with adaptive critic designs, in Proc. Artificial Neural Networks in Eng.
(ANNIE), ASME Press, 1996.
57 P.Werbos,
A hybrid hierarchical neural-AI model of mammal-like intelligence, Proc. SMC 1997, IEEE, 1997.
58 C.J.C.H.Watkins,
Learning From Delayed Rewards, Ph.D. thesis,
59 P.Werbos, Consistency
of HDP applied to a simple reinforcement learning problem, Neural Networks, March 1990.
60 P.Werbos, Building and understanding adaptive systems: A
statistical/numerical approach to factory automation and brain research, IEEE Trans. SMC, Jan./Feb.
1987.
61 P.Werbos, Optimization: A Foundation
for understanding consciousness. In D.Levine & W.
Elsberry (eds) Optimality
in Biological and Artificial Networks?, Erlbaum, 1996.
62. J.Houk, J.Davis & D.Beiser (eds), Models of Information Processing in the Basal Ganglia,
63. J.C.Houk, J.Keifer and A.Barto, Distributed
motor commands in the limb premotor network, Trends Neurosci.,
Vol. 16, p.27-33, 1933.
64. P.Werbos, Values,
Goals and Utility in an Engineering-Based Theory of Mammalian Intelligence, in
Karl H.Pribram, ed. , Brain and Values, Erlbaum:
65. B.Widrow and E.Walach, Adaptive
Inverse Control,
66. D.Prokhorov, Adaptive Critic Designs and Their
Applications, Ph.D. thesis.
67.
P.Simpson (ed), Neural Network Applications..
chapters
1-6.
68. P.Werbos, A Brain-Like
Design To Learn Optimal Decision Strategies in Complex Environments, in M.Karny, K.Warwick and V.Kurkova, eds, Dealing with
Complexity: A Neural Networks
Approach. Springer,
69.
L.Dolmatova and P.Werbos,
Traps and tricks in standard benchmark problems for neurocontrol.
In A. Meystel, ed., Proc. of 1997 Int’l Conf. on Intelligent
Systems and Semiotics,
NIST Special Publication 918.
70. T.Samad and W.Foslien, Parametrized neurocontrollers, Proc.
IEEE Int’l Symp. on Intelligent
Control (
71.
K.Krishnakumar and J.C.Neidhofer,
Immunized artificial systems -- concepts and applications. In Genetic Algorithms in Computers and Engineering,
NY: Wiley 1997.
72.
J.A.Suykens, B.DeMoor and J.Vandewalle, Nlq theory: a
neural control framework with global asymptotic stability criteria, Neural Networks, Vol. 10, No.4,
p.615-637, 1997.
73.
J.A.Suykens, J. Vandewalle
and B.DeMoor, Lur’e systems
with multilayer perceptron and recurrent neural networks: absolute stability
and dissipativity, IEEE Trans. Automatic Control, forthcoming (as of mid-1998).