Brain-Like
Intelligent Control: From Neural Nets to True Brain-Like Intelligence
Paul J. Werbos
National
Science Foundation, Room 675*
Arlington, Va.
22230
Abstract
This
past year has seen great progress in understanding stability and developing practical
applications for new learning control designs, originaly developed in the neural network area but applicable to
a wider class of designs. However, there is still a big gap between the best
designs implemented so far, and the kind of intelligence or higher-order
decision-making capability seen in mammal brains, and required for multilevel
control structures such as the management of entire factories or battlefields.
This paper will briefly cite some of the prior work, but mainly summarize a new
hybrid neural-AI design -- emerging from the underlying mathematics, rather
than ad hoc synthesis -- which has the potential to close that gap.[1,2].
The
new design draws heavily on concepts of hierarchy and temporal chunking from Artificial
Intelligence (AI), and on relational
representation of objects and space, and
a fuzzy goal representation.
Background: Learning
Control, Stability and Applications
Substantial
progress has been made in the past year
in developing applications, understanding stability, and improving key
subsystems of learning-based controllers [3]. Considerably more work is
needed in all these directions.
In conventional discussions, it
is often suggested that neurocontrol is essentially just an extension of
adaptive control, which in turn is seen as the antithesis of H-infinity or
robust control. (Robust control is a standard
approach in control theory, often attributed to Tsypkin, reviewed in [3].)
In actuality, this is extremely
misleading.
The most popular form of
robust control -- linear H¥ control, with no internal
feedback loops in the controller to
complicate the stability analysis -- provides high guarantees of stability, but
only under strong assumptions and for limited types of plant. There are many
practical situations where no controller can be designed in this family, which meet the full range of plausible
parameters of the plant. For example, in
building high-performance
hypersonic aircraft, a recent
study based on modern H-infinity design
tools revealed that the range of controller parameters which could stabilize
the plant when it has a center of gravity as 12 meters did not overlap at all
with the set which stabilizes the plant at 11.3 meters. Even if there are ways
to try to control the center of gravity, one would feel a lot safer if one
could also provide a more reliable control system.[3]
In such cases, common sense
tells us that we would be safer and
stabler, in practice, if we could somehow adjust the contrlller
parameters to reflect what the center of gravity actually is. There
ought to be some way to use
current information about the center of gravity which is better (in
terms of stability) than simply throwing out that information. In other words,
an adaptive control strategy of some kind ought to lead to greater stability
than ordinary robust control. But in practice, industry has found that this is
not true for the kinds of adaptive control available to them today; as a result
adaptive control is far less popular than simple robust control.
Why is it that adaptive control
does not seem to have the same advantages in practice that it ought to have in
theory? One reason is that the vast majority of work in adaptive control --
both classical adaptive control and neural adaptive control -- is based on
minimizing some measure of tracking error one period of time ahead into the
future. Substantial effort has gone into proving stability theorems for that
class of design; however these stability theorems impose very strong
assumptions, except in special cases where application-specific Liapunov
functions happen to be known. As a practical matter, it is very easy to get
into an overshoot instability when the proper direction of adaptation is
not known, because the direction of change which reduces tracking error one period ahead may be
opposite to what stabilizes the system many time periods ahead.
For this reason, the practical
industrial applications of neural networks in control tend to involve methods
which minimize error or cost many periods
of time ahead into the
future.
In
a sense, the practical applications found in industry tend to use more advanced
and brain-like designs than the ones which thereticians write about! There are
two broad classes of design which are popular here: (1) methods which involve a
direct simulation of future time-periods, and an explicit multiperiod
optimization of some kind (e.g. Neural Model-Predictive Control, NMPC 4]); (2)
methods which approximate dynamic
programming.
The first class of methods is
currently more popular in industrial applications, in part because it is
straightforward to implement, using the details given in [4,ch.8] and [5,ch.10].
This
kind of learning control has been implemented mainly with neural networks;
however, it would be straightforward to use
a modified, learning-based form of fuzzy logic to perform the same
task[6]. Usually, if one has the models and data required for offline learning with neural adaptive control, the
upgrade to [4,ch.8] should be very easy
and very effective; it provides an effective but quick fix to problems
involving timing and delays, which are rampant with the simpler forms of neural
adaptive control.
As an example of this approach.
representatives of a major US steel company recently told me that they now use
NMPC routinely to control some of their critical processes, and believe that
their competitors do so also (though many details are proprietary), based in
part on [5,ch.10]. Likewise, the first major success of Ford Research in using
learning control to reduce emissions was
based on a related approach (reviewed in [3]).
Ironically, however, the most
consistent way to minimize costs over many time periods does not involve an
explicit development of a future plan. Dynamic programming is the only
exact and efficient tool available to optimize into the future in the general
case, when noise or uncertainty is present. This class of methods is
also far closer to what we see in the brain than is NMPC[1,2].
In actuality, the more
advanced segments of the nonlinear
H-infinity community
have
actually been converging with the neural network community in pinpointing what
is really needed, for maximum stability: i.e. control designs which are based
on solving a stochastic optimization problem, using controllers which are
powerful enough to function over a wider variety of possible plant parameters.
In order to cope with a wide range of possible plants,
it is critical that the controller have the kind of “memory” which allows it to
represent implicitly such variables as “the current center of gravity.” In H-infinity,
this is typically done with “observer” components. In neurocontrol, it is done
by using time-lagged recurrent networks.
Either way, one can adapt the resulting complex controller by trying to
minimize some measure of error or cost, in an offline mode, across a wide range
of possibilities for how the plant behaves. I called this
strategy“learning offline to be adaptive online” when I first proposed it in
1990. Ford Research has developed a more specific approach to implementing this
strategy, which they call “multistream
learning” (reviewed in [3]).
Given
such a controller, the problem then lies in how to perform the adaptation.
Starting
in the 1970’s [7], I have developed a family of designs -- initially
implemented as neural networks -- for Approximate Dynamic Programming (ADP),
which have since been used, extended and popularized by a number of
researchers. In effect, the goal of
these methods is to approximate the Hamilton-Jacobi-Bellman equation as
accurately as possible, subject to constraints on computational effort and
hardware.
As
with NMPC, the main implementations have been based on neural networks so far,
but this is not required by the
mathematics. Likewise, both offline learning and online learning are possible.
As a practical matter, different
applications require different degrees of attention to stability versus other
measures of performance, In the ADP
approach, this is left up to the user.
It should be noted that the “J”
function approximated by these methods is also guaranteed to be a Liapunov
function. Thus, to the extent that the approximation is accurate enough, these
methods could be seen as a way of constructing a Liapunov function for
ordinary one-period ahead adaptive control.
ADP Versus Mammalian
Intelligence
By
1995, several groups of researchers had
finally implemented neural network designs which met certain basic criteria for
what a brain-like intelligence should look like[1]. These designs were intended
to be able to learn “any task” involving goal-directed behavior over time,
without prior knowledge of the task. In technical terms, such designs have been
called “model-based adaptive critics” or
model-based approximate dynamic
programming (ADP). They have sometimes been classified as a type of
reinforcement learning system. They permit much faster learning than more
primitive forms of rfeinforcement learning, at least when there are moderate or
large numbers of continuous variables which need to be controlled.
The engineering benefits of such
designs have become increasingly clear over the past few years. By now ten
groups have successfully implemented
such designs [2,8]. The strengths and weaknesses relative to conventional
designs, in terms of stability, etc., are becoming better understood [3]. In formal terms, these designs provide a
capability for optimization over time in uncertain noisy nonlinear
environments; that, in turn, permits systems to learn how to track a narrow
desired trajectory or performance
envelope, which is especially useful when trying to operate highly
dynamical nonlinear plants.
In many engineering applications,
neural networks are now used as part of a straightforward extension of ordinary
adaptive control. In effect, matrices are simply replaced by neural networks in
the same designs. In most cases, controllers are adapted so as to minimize square error in tracking at the next sampling time (t+1),
based on the use of derivatives propagated through some kind of plant model,
fixed or adapted. But neural net controllers using this approach have essentially the same problems with
delays and nonminimum phase plants that ordinary adaptive controllers have.
Using the exact same training examples, controllers designs and models, one can
usually achieve better performance and stability simply by taking a different
approach to training, based on multiperiod optimization. The explicit,
minimum cost n-period look-ahead approach
is explained in tutorial fashion in chapter 8 of [4] (which also
contains the original papers on backpropagation from 1974 and 1981). For a more
sophisticated and complete discussion,
see chapter 10 of [5]. This approach is not as popular in the journals as the
ordinary adaptive approach, but it accounts for a larger share of the success
in applications in industry.[3].
In 1970 or so, when I first
developed the theory behind the
model-based ADP designs, I hoped that
they would be enough to describe at least those aspects of higher-order intelligence
which exist in the mammalian brain. This is not the same thing as
explaining consciousness in the minds of humans. In order to understand consciousness
in the minds of humans, one must also address issues such as symbolic
reasoning, quantum computing and the soul, etc.; although I do have ideas about those subjects [9], they are beyond the scope of this paper.
In my view, a scientific understanding of the mammal-brain level of
intelligence is a prerequisite to a truly deep understanding of those more advanced
levels of intelligence[2,9]. Indeed, the new design to be mentioned here does
begin to provide some ideas about the deep
structure underlying verbs, nouns, and adverbs, at the very least.
Nevertheless, by 1996 [1], it
was apparent that these advanced designs
still had two major deficiencies -- major gaps between the kinds of learning
capability they provide, and the kind which exists in the mammalian brain.
First of all, in order to learn
many difficult planning problems, such as generalized spatial navigation, it would be necessary to
“fill in the boxes” in these designs with a certain type of slow but powerful
neural network, the “SRN.” [10,11]. To explain how the brain also
achieves high-bandwidth control of muscle movements, one then needs to assume a “two brains in one” master-slave
design described in [1].
Second, and more seriously, in
order to learn how to “see” far into the
future, the underlying learning rules have to be changed, to allow some sort of
“temporal chunking.” The usual critic
adaptation rules train a network at time t based on information about time t+1.
One can do far better by allowing the use of t+T, at times, where T is a larger
time interval. But how can one do this? My concerns about this were magnified
by the growing evidence from neuroscience that the basal ganglia are a crucial
part of higher-order intelligence, and that they perform something very similar
to task-based planning in AI[1].
A careful analysis of the
mathematics of temporal chunking in ADP forced me into the development of an
hierarchical task-based design, made up
of “decision blocks.” An international patent disclosure
was filed on this design on June 4, 1997, through Scientific Cybernetics,
courtesy of Sam Leven. The main specification section of that disclosure is being published in [12]. Of course, that
paper mainly deals with global implementation details. (The disclosure also
required 300 pages of additional papers
-- mainly papers previously published -- in order to describe
some of the subsystems.) In order to complement that discussion, another
paper is being published very soon [2] which summarizes the preceding history
and the intellectual strategy here in great detail. It expands on the
implications for neuroscience, stressing
the empirical data on the mammalian
brain.
I am very grateful to Alex
Meystel for drawing my attention to [13] , soon after the publication of [2].
This paper made me appreciate more seriously a third limitation of the
earlier model-based ADP systems -- their treatment of space. In a formal sense,
this problem can be handled without changing the higher-level architecture of
the model [2,12]. It is a subsystem issue, at least for the mammalian level of
intelligence. (But mammals do not have to coordinate 100 quasi-independent robotic
pieces of themselves spread out over an acre!) Nevertheless, the
required change in neural network
subsystems is very large, and has major implications for neuroscience [2] and
engineering applications[12]. It is particularly relevant to tasks like
predicting the behavior of molecules or controlling complex networks like heat
exchangers, precoolers, fuel processors, utility grids, etc.
A Few Details
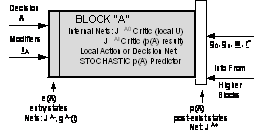
Figure 1. Structure of a
Decision Block
Figure
1 is a reduced version of a figure which appears in [2]. It summarizes the
structure of a
“decision
block.” In this theory, the upper level of the mammalian brain (excluding the
higher motivational systems) is essentially made up of a library of such
decision blocks. The blocks are formally distinct, but in practice (as in the
brain) they may share hidden nodes, and must share a common estimated state
vector R.
The task of each decision block
is to decide which lower-level decision blocks to activate. This is a
crisp, discrete decision. (In [1], I speculated that the activation might be
fuzzy instead of crisp; however, because of the problem of local minima, and
the need for rational learning, this did not turn out to be promising.) For the
lowest level block, the decisions are really just actions u sent to the lower brain.
Decision
blocks may be thought of as “active verbs.” The arrangement is strictly
sequential in nature, with only one decision block activated at any time on any
level of the hierarchy.
When a decision block is
activated, three kinds of additional information are also needed, to guide the
actions taken inside the block: “adverb” modifiers, a fuzzy goal object g,
and compressed information about the goals inherited from higher levels of the
hierarchy. In [12], mechanisms for adapting all of these structures or networks
are provided.
The fuzzy goal object mainly
consists of an image of a desired state r* plus a vector of weights
(indicating which components of that image vector are most important). In
effect, this object provides a kind of explicit quadratic representation of a
value function. The need for this kind of representation became clear only
after considerable analysis of the problem of communication between decision
blocks.
Crudely speaking, the benefit of
fuzzy goal images may be explained as follows.
In
essence, the choice of what decision to
make at time t depends (directly or
indirectly) on an evaluation of how good that decision would be; this
evaluation may be the output as a neural network, J’(decision, state(t)) or
Q(decision,state(t)), in the notation of [5]. That network, in turn, would be
trained to try to match or predict the
evaluation of the outcome, J(state(t+T)), where t+T represents the completion
of the decision block or action schema. In order to perform this training,
using simulated experience rather than
actual experience, one might use the
usual strategy of sampling -- of simulating what state(t+T)
might
be, based
on a stochastic simulation model which inputs decision(t) and state(t) and
outputs possible results. Alternatively, one might use a stochastic model
which, at least in part, outputs a kind of representation of the probability
distribution of state(t+T). (The R vector of the Stochastic
Encoder/Decoder/Predictor (SEDP) [5,ch.13]
is such a representation). Then, if the
estimate of J is forced to fit a functional form which is suitabel for this
purpose, it may be possible to calculate the expected J
by
doing closed form integration
instead of sampling. This eliminates the extra computational time and
error
associated with sampling. The fuzzy goal image
is one way of constraining the form of the estimate of J, consistent
with the form of probability representation generated by SEDP. In the 3-brain
design [12],
however,
additioanl fgeatures are present, to try to account for the gap between our
best estimate of J and
the
estimate we can realize in a fuzzy goal image; in effect, our vbalues J(t+T)
are decomposed into two parts, one of which (the goal) is highly explicit,
which allows for rapid replanning,
and the other of which
allows
for a more accurate overall
representation but slower planning.
Within each decision block,
neural networks must be adapted which are very similar to those in the usual
model-based adaptive critics -- local critic networks, a local Model or prediction
network, and a local Decision or action network. In this case, however, it is
especially critical that the latter two networks be stochastic networks, rather
than the usual sorts of deterministic neural network[2,12]. Two additional
networks are needed in order to optimize the interface with other decision
blocks.
A key aspect of using stochastic
networks is that one can replicate such phenomena as “imagination” or “dreaming” or
novelty-seeking behavior which is crucial to effective higher-order problem-solving and mammalian behavior [4,14].
References
1. P.Werbos, Learning in the
Brain: An Engineering Interpretation, in K.Pribram and J.King, eds, Learning as Self-Organization, Erlbaum,
1996.
2. P.Werbos, Values, goals and
utility in an engineering-based theory of mammalian intelligence, in K.Pribram,
ed., Brain and Values, Erlbaum 1998.
3. P.Werbos, Neurocontrollers,
in J.Webster, ed., Encyclopedia of
Electronics and Electrical Engineering, Wiley, (Feb. 1998).
4. P.Werbos, The Roots of Backpropagation: From Ordered Derivatives to Neural Networks and Political Forecasting, Wiley, 1994.
5. D.White and D.Sofge, eds, Handbook of Intelligent Control: Neural, Fuzzy and Adaptive Approaches, Van Nostrand, 1992.
6. P.Werbos, Elastic fuzzy
logic: a better fit to neurocontrol and true intelligence, J. Intelligent & Fuzzy Systems, Vol. 1, No.4, 1993.
7. P.Werbos,
Advanced fore-casting for global crisis warning and models of intelligence, General
Systems Yearbook, 1977 issue.
8. L.Dolmatova and P.Werbos, Traps and tricks in standard benchmark problems for neurocontrol. In A. Meystel, ed., Proc. of 1997 Int’l Conf. on Intelligent Systems and Semiotics, NIST Special Publication 918. Washington D.C.: GPO, 1997.
9. P.Werbos, Optimization: A Foundation for understanding consciousness. In D. Levine & W. Elsberry eds Optimality in Bio-logical and Artificial Networks?, Erlbaum, 1997.
10. P.Werbos & X.Z.Pang, Generalized maze navigation: SRN critics solve what feed-forward or Hebbian nets cannot. Proc. Conf. Systems, Man and Cybernetics (SMC) (Beijing), IEEE, 1996. (An earlier version appeared in WCNN96.)
11. X.Pang & P.Werbos, Neural net-work design for J function approximation in dynamic programming,Math. Modelling and Scientific Computing (a Principia Scientia journal), Vol. 5, NO.2/3, 1996. Available as adap-org 9806001 from xxx.lanl.gov/form using the “Other Groups” field set to “nlin-sys.”
12. P.Werbos, A Brain-Like Design To Learn Optimal Decision Strategies in Complex Environments, in M.Karny, K.Warwick and V. Kurkova eds Dealing with Complexity: A Neural Networks Approach. Springer, London, 1998.
13. J.Albus, Outline of Intelligence, IEEE Trans. Systems, Man and Cybernetics, Vol.21, No.2, 1991.
14. D.S.Levine and S.J.Leven,
eds, Motivation, Emotion, and Goal
Direction in Neural Networks, Erlbaum, 1992.