Values, Goals and Utility in an

Engineering-Based Theory of Mammalian Intelligence

 

Paul J. Werbos

 

National Science Foundation, Room 675*

Arlington, VA 22230

pwerbos@nsf.gov

 

 

Introduction and Strategy

 

                Values, goals and utility play a central role both in formal psychology and  in everyday life.

This paper will try to explain how our understanding  of these concepts can be further unified and enriched, based on a new engineering-based theory of mammalian intelligence[1].

                The new theory is essentially the latest iteration of an ongoing dialogue between neuroscientists like Karl Pribram and engineers like myself, each trying to grow beyond the usual limitations of these disciplines. A major goal of this effort is to bridge the gap between functional, realistic and intuitive descriptions of the brain and more formal mathematical, computational representations. After we develop a better understanding of how the higher-level functional abilities of the brain could be replicated, by certain types of parallel distributed computational structure, we will then be ready to do a more serious job of matching such structures to the lower-level features of neural circuitry and to suggest new experiments.

                The underlying  strategy of this approach has been discussed at great length in the past [2-4].

Those prior discussions have elaborated on issues such as the role of complexity, the importance of learning, the choice of mathematical tools, the strategies for experimental validation, and so on. Nevertheless, there are three strategic issues which need to be discussed yet again, because they are a source of concern to many researchers: (1) consciousness versus intelligence; (2) prior information versus learning; (3) neural networks versus computational neuroscience.

 

Consciousness Versus Intelligence

 

                The new theory tries to replicate the higher-level intelligence of the brains of mammals.

This is not the same thing as explaining consciousness in the minds of humans.

                Many of us are actually more interested in human consciousness, in principle, than in mammalian intelligence. For example, I have written at length about the various meanings of the word “conscious,” about the role of  human language and  symbolic reasoning, quantum computing, the soul, and so on[5].

However, those topics are beyond the scope of this article.

                I will argue here that a deeper  understanding of  mammalian intelligence is actually a prerequisite to a deeper  understanding  of  human consciousness, just as algebra  is a prerequisite  to calculus and calculus is a prerequisite to understanding  gravity. In reality, in everyday life, we have to develop some kind of intuitive understanding of gravity (dropping  things and breaking things) before  we even learn algebra . In the same way, intuitive studies of language and the soul can be very important to everyday life.

But for a  deeper understanding of gravity -- and of the higher levels of intelligence -- one must first master the prerequisites.

                In fact, the word “intelligence” actually  represents  one of the meanings of the word “consciousness” in everyday conversation.  Sometimes when we refer to systems as possessing “consciousness,” we  mean that they are intelligent.

 

_________________________

*The  views herein are those of the author, not those of NSF, though they are written on government time.

                Some authors who write about “consciousness” or “intelligent  systems” act as if consciousness were some kind of binary variable. They ask: “Is  it conscious or is it not?”, as if the answer should be “yes” or “no.” In  my  view, the question itself is fundamentally misleading. On the other, some classical behaviorists have treated intelligence as if it were a continuous variable, like the Intelligence Quotient. In the extreme form of that view, snails and humans are treated as if they are qualitatively the same, and different only in their speed of learning.

                Based on empirical reality, I would argue that “consciousness” or “intelligence” is actually more like a staircase -- a discrete series of levels, each level qualitatively different from the level before. (Actually, it is a tilty staircase, insofar as there are some quantitative differences  within each level, but these are not as important as the qualitative differences between levels.) The most important levels, for our purposes here, correspond  roughly to the classes of vertebrates -- fish versus amphibians versus reptiles versus birds versus mammals versus the symbolic-reasoning level of intelligence. These are the forms of intelligence that we actually see in nature.

                At a superficial level, the differences between different mammals seem very large. For example, the neocortex of a normal adult monkey contains many more visual areas than does the neocortex of a mouse. However, lower classes of vertebrate do not even possess a neocortex at all. Furthermore, the same underlying principles of learning seem to determine what is actually learned and stored in the various areas in the neocortex. When one area is damaged but the necessary connections are present, other parts of the neocortex can learn to take over the functions of the damaged area. There is a huge literature

on “mass action” and “equipotentiality” which has demonstrated this. (This literature originated in the classic work of Lashley, Pribram, Freeman and their colleagues.) For example, neurons in the temporal cortex have learned to take over as edge detectors in some experiments. The new theory to be described here [1] tries to replicate the underlying learning abilities which are essentially the same across all mammals.

                Years ago, in comparative psychology, Bitterman [6] demonstrated qualitative differences in the nature of learning across different classes of vertebrates. The details are beyond the scope of this paper, but did contribute to the development of our new theory.

                Many researchers in Artificial Intelligence (AI) have argued that “real intelligence” requires the use of symbolic reasoning. One such researcher begins his talks by asking how Einstein reasoned, in order to develop his theories. I would certainly agree that these are excellent examples of higher-order intelligence. However, I would question our chances of building an artificial Einstein before we can build even the crudest version of an artificial mouse. If Einstein and the mouse were unrelated phenomena, it might make sense to aim directly to build an Einstein, since he is more interesting; however, the symbolic reasoning used by Einstein and by other relatively intelligent humans is deeply rooted in the mammalian

neocortex and in other brain structures which we share with other mammals. There are good humanistic

reasons to try to understand symbolic reasoning better, even now, as I discussed above; however, a deep understanding of the neocortex and of mammalian intelligence in general should permit a much deeper understanding of symbolic reasoning as well in the more distant future.

 

Prior Information Versus Learning

 

                The new theory to be described here is a general purpose learning design. It can be

started out with essentially no concrete knowledge of its environment. Given time, it can develop a very complex understanding of its environment, and a complex plan of action, based entirely on learning from experience. The learning-based approach is now very familiar in the neural network field, where it has led to many practical, empirically-tested applications now being used in technology and in finance. The success of this approach has contributed to a resurgence of interest in learning even within hard-core AI.

                On the other hand, some AI researchers still speculate that learning-based designs by themselves

could never replicate higher-order intelligence such as what we see in the neocortex. They speculate that higher-order intelligence can only grow in the soil of very extensive, hard-wired prior knowledge which is very concrete and specific in nature. Certainly, in the nervous system, there are many lower-level sensory and motor circuits and reflexes which are very specialized and preprogrammed in nature. But some of these researchers go on to claim that much of the higher-order processing -- such as the entire path up from edge detectors through to object identification -- is preprogrammed in a concrete way. As evidence,

they argue that some mammals -- like ungulates -- are actually born fully functional, and able to perform these kinds of cognitive tasks, before they have had any time to learn anything. They even argue that much of the supposed “learning” in human infants may be part of a preprogrammed developmental

process, similar to what happens to baby ungulates in the womb, and independent of learning experience.

                This paper will not try to evaluate the last few claims, one way or another. But there is a crucial

logical point which needs to be considered: even if these claims should be true, even if there is substantial

concrete higher-order information born into the mammalian brain, this still does not imply a lack of ability to learn this same information if the occasion should arise.

                As an example, even if certain cells in the neocortex are set up as edge detectors, right from birth, this does not imply that neocortical cells lack the ability to learn edge detection, through ordinary learning from experience. In fact, the temporal lobe experiments mentioned in the previous section clearly demonstrate that these cells do possess that learning ability.

                There is no real paradox  here. In practical engineering applications, one often initializes the weights and connections of an artificial neural network (ANN) to the best available initial guess, based on the available prior information, even though these same weights and connections will then be adapted

freely as if they had been the result of learning. There is no special reason to initialize the weights to zero.

One would expect evolution to use the same general sort of opportunistic approach, combining both

prior information and a generalized learning ability, to the extent that the machinery of DNA permits

the transmission of specific information.

                All forms of learning do tend to make some sorts of prior assumptions about the world, implicitly, of a very general theoretical sort [7, ch.10]. The new theory to be described here is no exception. However, it does not require extensive, concrete forms of prior knowledge, of the sort which is

popular in the world of expert systems in AI.

 

Neural Networks Versus Computational Neuroscience

 

                The new theory to be described here is quite different in flavor from the usual differential equation models which are most familiar in neuroscience. It results from a modeling approach very different from conventional computational neuroscience. This section will discuss these differences, somewhat briefly and crudely, in order to help the reader understand how these different approaches are

complementary.

 

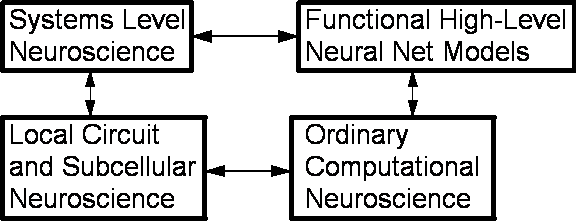
Figure 1. Some Major Strands of Research Addressing Mammalian Brains

 

                Figure 1 provides a crude overview of some important strands of research which try to understand the mammalian brain. Research involving invertebrates, etc., is beyond the scope of this paper. The chapter by James McClelland in this book probably belongs in a new box on the middle right,

but that too is beyond the scope of this paper.

                On the left side of Figure 1 are two boxes representing two important trends in neuroscience which have had an uneasy coexistence for decades. Systems level neuroscience addresses higher-order issues such as the functional significance of major parts of the brain, the representation of emotions in the brain,  the location and dynamics of working memory, the interaction between the neocortex, the limbic system and the basal ganglia, and so on. It attempts to understand fundamental issues such as the nature of human intelligence and motivation, through qualitative analysis of extensive clinical and experimental

information. It tries to account for experimental information from lower levels, but the major focus is on understanding the whole system. Karl Pribram has been one of the serious contributors to this field for decades.

                Local circuit and subcellular neuroscience operates at a very different level. This area has had a tremendous spurt of growth in recent decades, due to the development of genetic technology and other new technologies which tell us more and more about the molecular events involved in some forms of learning, about connections between neurons, and so on.

                Many neuroscientists believe that the main challenge to neuroscience as a whole is to explain the higher-level phenomena in terms of the local circuit and subcellular phenomena. In other words, the challenge is to connect the two levels of analysis more completely.

                On the other hand, many other neuroscientists believe that the key challenge to the field is to put the whole field on a more precise, more mathematical footing. Their goal is to become more like physics, in some sense. These neuroscientists have developed more and more differential equation models -- some rooted in extremely detailed physics and chemistry -- which attempt to describe local circuits very precisely. By building up from such models, at ever higher levels of abstraction, they have also built up to models which actually try to replicate meaningful mental functions, such as associative memory or early vision in the adult.

                The theory to be described here fits into the upper right box, which is currently the most sparsely populated part of this figure. Rather than modeling the brain from a bottoms-up point of view, it takes a top-down approach. It tries to provide a mathematical articulation or model of the kinds of phenomena  which neuroscientists like Pribram have focused on, rather than articulating subcellular phenomena.

                In the long term, I agree that the central challenge is to connect the two levels -- to develop detailed neural network models which match the subcellular data and the systems level information, both at the same time. There is a great need for researchers in the upper boxes and in the lower boxes to study each others’ work, in order to strengthen the effort to build a bridge between the two levels. On the other

hand, there is also a great deal of important work to be done in reinforcing the foundations at either side of the bridge. Particularly in the upper right box, the ideas are so new that considerable effort will be needed to sharpen, validate and consolidate the theory to be described here.

                In the upper right box, the focus is on higher-level functionality. The goal is to develop neural network models which replicate higher-order learning-based intelligence -- not just a component of intelligence, but the whole system. Thus the lower right box tends to draw most heavily on chemistry and physics, while the upper right box requires a heavy emphasis on engineering. Please bear in mind that “engineering” does not consistent of a collection of clever monkeys; it is a large, long-standing intellectual endeavor, which has developed rigorous mathematical techniques addressing the issue of functionality -- of understanding what works, what does not, how to develop new designs, and how to understand a wide variety of challenging tasks. Engineering concepts and engineering testbeds provide a very crucial intellectual filter and empirical testing ground for allegedly functional designs -- including designs in the upper right box.

                Most models used in engineering or in the artificial neural network (ANN) field do not fit within any of the boxes in Figure 1, because they try to achieve functionality in more limited kinds of tasks. Nevertheless, the theory to be described here was developed within the disciplines of ANNs and of engineering, because of the filters which they provide.

                How important are these filters? As of 1995 [8], only one class of neural network model had ever been implemented which met four basic necessary tests for a model of brain-like intelligence: (1) demonstrated engineering functionality, for a completely learning-based system; (2) possession of an “emotional” or “values” component, enabling the system to learn to pursue goals effectively over time;

(3) possession and use of an “expectations” component, as needed to address behavioral experiments in classical conditioning; (4) the ability to take physical actions (e.g. control motors or muscles).

These are necessary tests, not sufficient tests, but, when applied together, they rule out all the other models, including those which have emerged from computational neuroscience.

                Models in this class have since been adapted and extended to a considerable extent, in order to cope with difficult engineering control applications [9,10]. As a result of subsequent analysis -- both engineering analysis and the study of issues raised by Pribram and others -- these models are now essentially obsolete as models of mammalian intelligence; new, more complete models have been developed. However, the original models have still played a crucial role because: (1) by showing how it is possible to meet the four tests together, they opened the door to the development of more complex models in the same general family; (2) because they embody difficult control concepts in a simple context, they are crucial to our ability to really understand and develop more complex models embodying the same principles; (3) as testable, implemented designs they continue to provide a flow of empirical information about what works and what does not, and about the interface between higher-level models and lower-level components.

 

The Larger Context: The Role of Values  and Utility

 

            The new theory [1] is a theory of intelligence. But the mammalian brain includes more than just intelligence. Even before I began to develop serious designs for intelligent systems, decades ago[2], I started out by defining a working picture of how the intelligence fits in as part of the larger system [2,

11]. This picture is illustrated somewhat crudely in Figure 2.

 

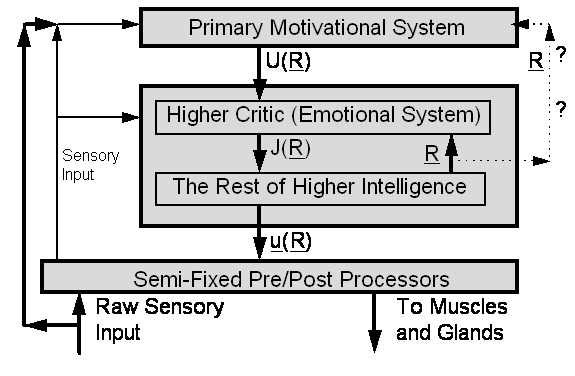Figure 2. Intuitive Picture of What the Brain Does

 

                In Figure 2, the intelligence proper consists of one big box containing two boxes inside of it -- the higher Critic and “the  Rest.”

                In this picture, the intelligence proper builds up an image or representation of the present state of the world, denoted by the vector R. The Primary Motivational System (PMS) provides a utility function,

U(R). The job of the intelligent system is to develop a strategy for how to maximize U, over the long-term future, by manipulating the actions which it controls. The choice of actions is represented by another vector, u. Below the level of higher-order intelligence -- which is based on truly generalized learning dynamics -- there are more or less fixed preprocessors and postprocessors, such as the retina, the motor neurons in the spine, and even the “motor pools” in the brain stem[12]. These lower-level systems often do contain some kind of adaptation abilities, responsive to higher-level actions (u), but their adaptation tends to be somewhat specialized in nature.

                Of course, this picture owes a lot to the classical work of Von Neumann and Morgenstern[13],

which in turn was essentially just a mathematical formulation of ideas from John Stuart Mill and Jeremy Bentham. Von Neumann’s notion of “utility function” is well known in economics, but somewhat less so in other disciplines. “Utility,” in Von Neumann’s sense, is not a measure of the usefulness of an object.

Rather, it is a measure used to evaluate the overall state of the entire world, R. (But see [3,4] for discussion of marginal utilities and prices.) Utility is a global measure of “success” or “performance,” or

any other “figure of merit” which an intelligent system tries to maximize. It represents the most fundamental desires or “needs” of the organism, as discussed in the chapter by Pribram in this book.

                All across the social sciences, there have been very rabid debates for and against the idea that people maximize some kind of utility function. In this picture, the organism is not assumed to do a perfect job of maximizing utility; rather, it is assumed to learn to do a better and better job, over time, subject to certain constraints which limit the performance of any real-world computing system. Perhaps the most important constraint is the need for a balance between play or novelty-seeking behavior, versus the danger of becoming stuck forever in a “rut” or in a “local minimum.” See [5,14] for more discussion of these issues.

                The utility function U(R) is not the only measure of value depicted in Figure 2. There is also another function, J(R), which is learned by the intelligent system proper. This function J(R) provides a kind of immediate strategic assessment of the situation R. The network which outputs J is called a “Critic” network.

                The need for the Critic network emerges directly from the mathematics, which I will discuss in more detail below. Intuitively, however, the J function corresponds to the learned preferences discussed by Pribram in his chapter in this book. (See [3,4] for more discussion of this intuition.)

                Following this picture, there are really four fundamental issues we need to consider when we try to understand “values”:

 

       (1) How does the Primary Motivational System work? Where do the basic “needs” come from?

       (2) How does the Upper Critic work? Where do our learned hopes and fears and preferences come from?

       (3) Are there other measures of value in the “Rest of System,” and, if so, how do they work?

       (4) Going beyond science, how can we as human beings do a better job of formulating and implementing our values, in light of this information?

 

                Most of the chapters in this book, like most of my own published work, focus on “values” in the sense of question 2. They focus on the effort to understand the higher levels of intelligence as such, including the learned emotional associations in the main part of the limbic system. The new theory [1] addresses questions 2 and 3.

                Nevertheless, as Pribram points out, the PMS is more fundamental and more universal, in some sense. It is the foundation on which the rest is built. Better intellectual understanding can logically supersede what we have learned from experience (questions 2 and 3), but it cannot supersede the PMS.

                In my own work, I have discussed the PMS somewhat, mainly on a theoretical basis [2,5].

At this conference, Allan Schore gave an impressive talk on the process of imprinting, which is crucial to the dynamics of the PMS. The PMS obviously includes some fixed systems in the hypothalamus and epithalamus, which respond to a wide variety of simple variables like blood sugar, pain, and so on.

As Pribram points out, it often includes simple measurable variables which serve as indicators, in effect, of concepts which are more important to the organism but harder to measure. The PMS also includes some fairly complex social responses, as described by Schore, based in part on something like an associative memory. This is not the kind of associative memory which one uses as part of a utility maximization scheme; rather, it is a special kind of associative memory, with laws of its own, which requires more of an empirical approach to understanding.

                The remainder of this paper will describe the new theory of intelligence, which includes a response to questions 2 and 3. For the sake of completeness, I will conclude this section with some thoughts about question 4.

                Question 4 really raises the larger questions of ethics and of the concrete goals we pursue in our lives and in our society. In the past [5], I have argued that a sane and sapient person would gradually learn a two-pronged approach to these issues: (1) improved self-understanding, by learning, in effect, what one’s own PMS is really asking for (U); (2) a thoroughly systematic, intelligent effort -- supported by a synergistic use of symbolic reasoning and focused intuition -- to go ahead and maximize one’s U over the long-term future, over a large playing field. Broadly speaking, this is consistent with the spirit of Pribram’s comments in his chapter as well. Both prongs of this approach encourage us to learn to “see” all inputs to our consciousness -- including the emotional inputs -- in the same focused and intelligent way that many of us reserve for visual inputs only.

                Certain cultural authorities would consider this approach extremely threatening. When people think for themselves, they may become harder to predict and control. However, these fears indicate a disrespect for human intelligence and a short-sighted effort to maximize the authorities’ own power.

(Indeed, such authorities have been known to foster illiteracy and the use of drugs in order to advance their allegedly higher ethical values.) As our environment becomes more and more challenging, and more and more dependent on the honest and creative management of complex information, such static, repressive and authoritarian attitudes become less and less consistent with human survival.

 

Description of The New Theory

 

Introduction

 

                The new theory can be seen as a hybrid between hierarchical task planning, as practiced in AI, and neural network designs based on reinforcement learning or adaptive critics. In effect, the task planning aspect provides a way to operationalize the classic theory of Miller, Galanter and Pribram[15].

The neural network aspect provides a way to link the system to higher values and emotions, and to the brain. The design as a whole provides a unification of these two different approaches or aspects of higher-level intelligence.

                The new theory is a natural outcome of earlier theories and concepts discussed in [3]. The details of the new theory were first reported as part of an international patent application filed on June 4, 1997. The main design-specification part of that disclosure was included in [1]. Links to biology are mentioned in [1], but they are sandwiched between discussions of the engineering details, which are quite complicated. This paper will not reproduce all of those details; instead, it will try to explain the points of greatest importance to biology and psychology.

                Even one year ago, I had no intention of devising a theory which is strictly and classically hierarchical in nature. The concept of hierarchy has been used all too often as a quick ad hoc solution in AI, and it often limits the learning capability and flexibility of the resulting design. However, the seminal work of Vernon Brooks on motor control[16] makes it clear that some hierarchical approaches can still be

compatible with parts of the biology. In the end, a careful study of the mathematics [1] have me no choice, and it also provided a basis for incremental, neural-style learning in such a system.

                In my present view, the new theory fits the mammalian brain in much the same way that certain line drawings can fit an oil painting. Often, before an artist paints an oil painting, he first draws a cartoon-style, black and white sketch of the same scene. The contours are all there, and all the objects are there, but the colors and the fine texture all have yet to be filled in. In the same way, the new theory -- as an engineering design -- actually involves several choices between possible subsystems. New subsystems will be needed, in the future, in order to improve performance and in order to fit the lower-level details of the brain more exactly. Nevertheless, this theory -- unlike its predecessors -- does seem to encompass all the major higher-order structure which needs to be filled in. The work ahead of us is less like running ahead into the wilderness, and more like settling in and developing known territory.

                The work leading up to the new theory has already been published in the past. However, a certain degree of condensed review is necessary, to make this paper at least partly self-contained.

 

Relation to Prior Theories: Concepts and History

 

                The new theory, like its predecessors, is a general purpose learning system. Like its predecessors, it is  designed to learn how to develop a strategy of action which will maximize some externally specified utility function, U, over all future times. Expressed as an engineering design, it is a system which learns how to perform optimization over time. It is intended to operate in a generalized manner, such that it could learn to perform “any task,” based on learning from experience, without concrete prior knowledge of the task. This family of designs is sometimes referred to as “reinforcement learning systems,” but it is more accurate to call them “adaptive critic systems” or “approximate dynamic programming” (ADP).

                If the new theory and its predecessors both perform this same function, then what is the difference between them? There are two important differences. First, the new design contains new features which substantially expand the range of tasks which can be learned in a practical way, at a reasonable learning speed. Second, these features provide a more complete fit to global features of the brain.

                Decades ago, when this work began, I was impressed by the work of Hebb[17], who seemed to suggest that higher-level intelligence could emerge from the operation of a simple, general learning rule, operating across all neurons in the brain. That simple vision simply did not work out in functional or engineering terms, and it never provided any kind of explanation for the major structural components of the brain. Later, a variety of “reinforcement learning” models or designs were developed by several

authors [11,18,19]; however, none of them met the simple four tests for a brain-like system mentioned in the Introduction above and discussed at length in [5]. This section will only discuss designs which do at least meet those minimal tests.

 

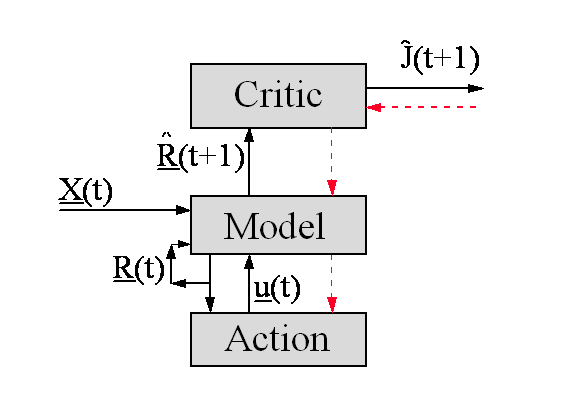
Figure 3. The Earliest “Brain-Like” Control Design

 

                Figure 3 illustrates the simplest design in this family. In this design, there were three major components of the overall “brain.” The highest was the emotional system or “Critic,” whose task was to estimate the function “J” discussed above. I associated the Critic with the limbic system of the brain.

The middle was the “Model” -- a neural network trained to act as a simulation model of the environment of the organism. (Following standard engineering approaches, the Model also calculated an “estimated state vector R”, i.e. a representation of the current state of the environment.) The Model served, in effect, as an expectations system.  I associated it with the cerebro-thalamic system. Finally, the system also contains an Action network -- a network trained to output control signals u, which affect muscles, glands and the orientation of sensors.

                The mathematics of how to adapt this system were first developed in 1970, first published in 1977[20], and explained more completely in 1992 [7]. The first practical engineering test, in simulation,

was published by Jameson in 1993. By 1995, three additional groups -- Santiago and myself, Wunsch and Prokhorov, and Balakrishnan -- had implemented, tested and published more advanced designs of the same general flavor[8]. In a 1977 conference [9], four new groups reported implementations, some with substantial practical significance -- Ford Motor Company, Accurate Automation Corporation, Lendaris and Tang. Dolmatova and myself, working through Scientific Cybernetics, Inc., have developed some new implementations, which will be published elsewhere in 1997. In addition to these nine groups in the United States, one researcher in Sweden -- Landelius [21] -- has also had important results. Even the simple design in Figure 3 is substantially more complex than the underlying designs used in the past in control engineering; however, as we develop more understanding of its practical capabilities relative to earlier control designs [10], the practical use of this family should continue to grow.

                In Figure 3, the broken arrows represent a flow of value information, which is crucial to the dynamics of learning in this design. The overall design given in [7, chs. 3 and 13] does not specify what kinds of networks to insert into these boxes. It deliberately gives the user or modeler some flexibility in that regard. However, it does specify how to calculate the flow of value information, for any choice of network, and how to use that information in adapting the Critic and the Action network. (A different

chapter -- [7,ch.10] -- discusses the structure and dynamics of learning for Model networks.) Those value

calculations turn out to match exactly the rules for the “flow of cathexis” proposed by Freud years ago [2,3]. The same underlying algorithm which I developed for that application is now being used in most

practical applications of ANNs, both in technology and in finance[2].

                Back in 1970, I hoped that this kind of design would be enough to replicate higher-order intelligence. If the three boxes were filled in with simple neural networks, each made up of one class of neuron, then Hebb’s dream would almost be fulfilled. Instead of one “general neuron model,” one would need three general neuron models, one for each class of neuron. One would also have a basis for understanding the division of the brain into major components [2,3,22].

                Over the years, this hope had to be modified. Engineering research told us more and more about how to “fill in the boxes.” It told us that we need to fill in the boxes with fairly complex structures, in order to get maximum performance [7]. Instead of three cell types, the research pointed towards a need for boxes within boxes, ultimately leading to dozens and dozens of basic, generalized cell types. But this did not invalidate the overall model, at first. In fact, it led to an improved fit with neuroscience; for example, it began to suggest an explanation for some of the more detailed features of the cerebro-thalamic system[3].

                By 1992, however, this study of substructures had led us to a major paradox [7,23].

We discovered that many higher-order learning tasks require us to fill in some of the boxes with a certain class of neural network -- the Simultaneous Recurrent Network (SRN) -- which requires many iterations in order to settle down and calculate its output [24,25]. This slow speed of calculation is inconsistent

with the requirement for fast calculation (circa 100-200 cycles per second) for the smooth coordination of bodily movements.

                To explain this, I then proposed a “two brains in one” [3] theory of the mammalian brain. According to that theory, the brain contains two entire adaptive critic learning systems, each with its own Critic network. In the upper brain (limbic system and cerebro-thalamic system), the relevant boxes are filled in with these slow but powerful SRN components. Thus the upper brain performs a major cycle of computation over a relatively long time period -- 0.1 to 0.25 seconds, corresponding to alpha or theta rhythms. (Within that period, it goes through many minor iterations, as required by the SRN model and verified by recent multichannel EEG recordings in Pribram’s laboratories.) The lower brain (mainly the

olive and cerebellum) uses simpler, more feedforward components, which allow it to operate at a faster rate. The lower brain is trained, in effect, to try to make the upper brain happy.

                All of these theories had one really large, gaping hole in them: the lack of an explanation for the role of the basal ganglia. Decades ago, this did not seem like such a big hole, because the importance of the basal ganglia was not yet so well understood. But evidence has begun to accumulate [16,26,3,4] showing that the basal ganglia do indeed play a crucial role in the brain. Fortunately, this role also seems to be related to certain functional weaknesses of the earlier theories as well. It seems to involve the organization of time or “tasks” into large blocks or “chunks,” which make it easier for the system to do long-term planning. Thus once again, by working to improve the functional capabilities of our theory, we can expect to converge more closely to neuroscience as well. For the complete form of our new theory, we also revisit the treatment of space, which immediately suggests new interpretations of some well-known information about vision in the neocortex.

 

Relation to Prior Theories: Basics of the Mathematics

 

                The new theory continues to assume that there is a kind of master-slave relation between the “upper brain” and the “lower brain,” as in [3].  It replaces the old picture of the upper brain with something far more complex.

                The previous picture of the upper brain was still essentially based on Figure 3 (with various elaborations discussed in the engineering literature[5]). Figure 3, in turn, was originally derived from an effort to approximate dynamic programming. Dynamic programming is the only exact and efficient general-purpose algorithm available to calculate the optimal strategy of action over time in an uncertain, noisy, nonlinear environment.

                In dynamic  programming, the user supplies a utility function U(X) and a stochastic model to

predict X(t+1) as a function of X(t) and u(t), where X denotes the present state of the environment and u denotes the actions taken by the controller at time t. (For simplicity I will assume that the state of the world as seen by the senses, X, is the same as the actual state of the world, R; however, the difference between the two is an important part of the theory.) Our task, in control, is to find the optimal strategy of action u(X). We do this by solving the Bellman equation:

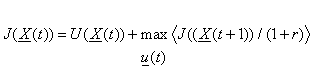                        (1)

 

where the angle brackets denote expected value, and where this “r” is a kind of interest rate which can be

set to zero for now. Our task is to find a function J(X) which satisfies this equation. According to the theorems of dynamic programming, the optimal strategy u(X) can be found simply by picking the actions which maximize <J(X(t+1))>, exactly as in equation 1.

                Pure dynamic programming is not useful even in medium-scale control applications, because it is simply too difficult to find an exact solution to equation 1, in the general case. In approximate dynamic programming (ADP), we try to learn an approximate solution. In the simplest forms of ADP, we approximate the function J by some network J(X,W), where “W” represents the set of weights or parameters (e.g., synapse strengths) in the network. The goal is to adapt the weights W, so as to make J(X,W) fit equation 1 as closely as possible, in some sense. The equations used to adapt the weights W effectively imply a theory for how the synapse strengths are adapted over time in the corresponding biological neural network.

                In the simplest previous theory, the Critic would be adapted as follows. At every other time t, we would remember X(t), and then wait until time t+1 before performing adaptation. At time t+1, we would calculate J*=U(X(t))+J(X(t+1)). Then we would go back to considering X(t). We would adjust the weights W so as to make J(X(t),W) match more closely to J*. I called this approach Heuristic Dynamic Programming (HDP) when I first published it in 1977 [20]; however, it was rediscovered in 1983 under the name “Temporal Differences”[18].

                There are many variations of this approach, but the ones which work all have the same general effect: they update the estimate of J(t) so as to account for information one time period ahead, from time t+1. In effect, after training, the organism “sees into the future” one time period further than it did before learning. But if one time period is a very short interval of time (such as 0.25 second!), this may not be much of an improvement in foresight. Furthermore, it would take considerable training, over many possible states X(t), before the system could look ahead one time period further across all of these possible states.

                This “foresight horizon problem” is not new. I discussed it, for example, in [27,28].

There are many ways to try to improve the degree of foresight, even for this class of designs; some of these approaches seem quite promising, while others have been proven incorrect [7,28]. Nevertheless, whatever tricks or design modifications one uses, there is no substitute for the simple effort to use “t+T” in place of “t+1,” where T is a larger time interval. More precisely, by using “t+T” instead of “t+1,” in addition to other design improvements, we can still expect to achieve much greater foresight. The problem lies in how to do this, within the framework of a learning-based neural network design. The new theory provides a solution to this problem. In AI, this problem is commonly referred to as the problem of “temporal chunking.”

                Another major deficiency of the previous theories concerns the treatment of space. In AI, for example, the problem of “spatial chunking” has received a lot of attention. John Holland has talked about road maps as an example of a compressed representation of space. Albus [29] has discussed the problem of coordinating the actions of diverse robots spread over a large region of space such as a factory floor.

                Even in the new theory, the treatment of space is seen as a subsystem issue. In principle, it does not affect the highest-level structure of the mathematical theory. Individual mammals, unlike factory management systems, are not really spread out over a large region of space. Humans and other mammals are not 100% flexible about “doing two things at the same time.”

                Nevertheless, the treatment of space really does have some pervasive implications. There are some basic principles of symmetry which have been exploited very effectively in the image processing part of the neural network community [30,24,25], but largely ignored in other parts of the community.

The new theory assumes that the brain exploits a similar but more general form of symmetry, which I call “object symmetry”[1]. In essence, object symmetry simply predicts that objects will behave the same way, as a function of their relations to other objects, regardless of where they are physically located or seen. It is extremely important to exploit this principle, when trying to adapt to a very complex environment which contains thousands of significant objects and locations in it, but traditional neural networks do not do so.

                In principle, there are three ways to train neural networks to exploit object symmetry. One way is to broadcast connections and weights from a “master copy” of a small neural network; this is not biologically plausible, in my view. Another way involves the use of special tricks to encourage separate but similar regions to learn the same relationships; for example, rapid eye movements may result in many areas in visual cortex scanning the same object, and learning from it. In my view, this kind of parallel learning is an important part of what happens in neocortex; for example, it explains the ability of adults to classify all the letters in a word at the same time, in parallel, in one major cycle time (circa 0.1-0.25 second). On the other hand, such parallel training does not exploit the full theoretical potential implied by symmetry; it requires a lot of learning experience.

                The third approach is multiplexing -- the use of the same network, at different times, with different inputs, in order to recognize and predict different objects, accounting for their relations to a few related objects. The literature on dynamic feature binding in visual physiology strongly suggests that the brain does exploit the multiplexing approach, particularly in the regions of temporal cortex which recognize objects and (in humans) link up to the nearby speech centers. A key part of the new theory deals with methods for defining and adapting networks which map back and forth between ordinary vectors X and structures made up of objects and relations obeying object symmetry [1]. This in turn would have substantial implications for the organization of neocortex and hippocampus.

                In the brain, this approach highlights the need for the organism to maintain a kind of global “world model” [29] or inventory of objects in associative memory, even as the organism really focuses on one (or a few) objects at any time. Fukushima [9] has presented a theory of how this might be done, by patching together visual images, but his theory does not exploit the links between images and places which are crucial to optimal performance. In our theory, we can use essentially the same sort of architecture, except that visual images are replaced by a cluster of objects and relations. Because such

a cluster would include links between specific objects or places, better performance could be expected.

 

Temporal Chunking: Reasons for a Task-Oriented Approach

 

                Strictly speaking, temporal chunking presents an opportunity, not a problem. The conventional t/(t+1) designs do converge, in theory, to an optimal strategy -- eventually. My claim is that new designs, exploiting temporal chunking, can converge faster, when foresight over long periods of time is required.

                In classical AI, there are two common forms of temporal chunking -- multiresolutional or clock-based approaches, and task-based or event-based approaches. This section will try to explain, a bit more precisely, why these approaches can improve foresight, and why the task-based approach is probably preferable.

                For simplicity, consider the situation of an environment which can only exist in N possible states, where N is finite. Thus the state of the environment at any time, t, can be represented as some integer i

between 1 and N. Consider the situation where the strategy of action u(i) is fixed, and we are simply trying to learn/approximate the function J(i). For more explanation of this simple case, see [30,31].

                In this situation, the utility function U can be represented as a vector with N components, U1 through UN, where Ui is simply U(i). Likewise, the function J(i) can be represented as a vector J. The model of the environment simply consists of a set of numbers, Pij , representing the probability that the environment will occupy state i at time t+1 if it was in state j at time t. P is just a matrix of transition probabilities, and is called a Markhov chain. Let us define M=PT, the transpose of P.

                In this situation, the J function used in the Bellman equation has a simple representation:

 

                                J  =  U  +  MU  +  M2U  +  M3U  + ...                   (2)

 

The first term on the right represents the utility U in the current state (time t), the second term represents the utility in the next state (time t+1), and so on. (Roughly speaking, if X(t+1)=PX(t), then UTX(t+1) =

UTPX(t) = (MU)T X(t).) J represents the sum of utility over all future time periods, which is what we really want to maximize. From equation 2, we may immediately deduce the Bellman equation for this special case:

 

                                J  =  U  +  MJ                                                                        (3)

 

The usual adaptive critic methods basically approximate an old update rule discussed by Howard [30]:

 

                                J(n+1)  =  U  + MJ(n)                                                               (4)

 

This states that our n+1-th estimate of the J function is based on the n-th estimate as shown in this equation. If we initialize J(0) to equal U, then it is easy to deduce that:

 

                                J(n)  =  U  +  MU  + ... +  MnU                                               (5)

 

In other words, after n such very large updates (each accounting for every possible state of the environment!), our J function “sees” only n steps into the future.

                In matrix algebra, there is a much faster way to calculate the same sort of result. We

may write it as:

 

                J(n)  =  ... (I + M8)(I + M4)(I + M2)(I + M)U  (6)

 

(As an example, notice how (I+M4)(I+M2)(I+M) = I+M+M2+M3+...+M7!)

This sort of update procedure allows us to see more than 2n time periods into the future

after only n updates! Foresight grows exponentially, not linearly. The price is that we need to

compute the matrices M2, M4, etc. But notice what these matrices represent! (M8)ij , for example,

simply represents the probability of ending up in state i at time t+8, if you start out in state j at time t. These matrices are simply predictive models of the environment, jumping ahead 2 time periods, 4 time periods, etc. Thus equation 6 simply represents the classical idea of multiresolutional analysis, based on models that predict over large but fixed time intervals.

                In the real world, however, there is a serious problem here. First of all, it is hard to imagine a biological basis for such an arrangement. Second of all, the original matrix M will usually be extremely sparse, but the matrix Mk for large k will tend to be fully connected. If we do not somehow exploit the sparsity of M, then we do not achieve the full potential for cost reduction and efficiency.

                In developing the new model, I began by assuming that the states of the environment can be divided up into blocks, A, B, etc. This led to a modified Bellman equation which can be written,

crudely, as:

 

                                JA  =  JA0  +  JAIJA+,                                              (7)

 

where JA represents the J function for states within block A; where JA0 represents the payoffs (U) to be expected in the future within block A, before the system next exits that block; where JA+ represents the J function for states immediately outside block A, which I call the “postexit” states of A; and where JAI is a kind of connection matrix.

                In order to learn J most effectively, one can begin by learning JA0 and JAI within each block; this learning is done on a purely local basis, because it does not require knowledge of anything outside the block. Then, after these “local critics” have been adapted, one can use equation 7 to propagate values backwards from the end of the block (JA+) to the initial states at the beginning of the block, which also serve as the postexit states of the previous block. In other words, equation 7 can act like equation 4, except that an update jumps over the entire time-history of a block in one direct calculation.

                To make full use of this kind of procedure, one needs to develop a hierarchy of blocks within blocks (somewhat analogous to equation 6). One also needs to consider how we have a choice between blocks or tasks, at certain times. In reality, the choices we face are often very discrete  in nature. (Consider, for example, the choice of where to place the next stone, in a game of Go.) Because they are discrete choices -- each representing a kind of local optimum -- we need to use a crisp, discrete decision-making system, very different from the incremental and fuzzy value systems which work best at the highest and lowest levels of the brain. (Actually, the new theory does allow for fuzzy and incremental decision

making at the middle level, within each decision block.)

                The greatest challenge in developing the new theory was to find a smooth and effective approach to approximating this kind of design with neural networks, and to maintain a learning-based approach throughout.

 

 

 

Overview of the Structure

 

 

Figure 4. Structure of a Decision Block

 

                According to the new theory, the “middle  level” of the brain is made up, in effect, of a library of “decision blocks,” illustrated in Figure 4. In principle, each decision block is separate from every other block; however, as in any neural network design, a sharing of hidden nodes and of inputs is allowed.

                Each decision block has a “level.” When decision block A is activated, it then has the job of deciding which lower-level decision block it should activate. The system is sequential. In other words, at any given time, only one block is activated at any level; however, new decision blocks can be constructed as the attempt to activate two unrelated blocks on the same level at the same time. (Usually, however, it takes some time for the system to learn how to do two specific things at once in a smooth manner.) In the brain, the “level” would probably correspond to the level of the relevant loop in the neocortex-basal-thalamus reverberatory circuit, as described by Brooks [16]. (In theory, however, there could also be a kind of linked-list connection between a decision and its subordinate.)

                The trickiest part, in any decision block, is how to modulate the actions in that block, so as to better account for what later decision blocks will want after the current task is completed. This is done by providing the secondary decision information suggested in the figure: “adverbs” uA, a fuzzy goal image g, and some sort of condensed representation of longer-term goals. In effect, this information provides a kind of condensed representation of the vector JA+ of equation 7. The fuzzy goal image approximates J, in effect, as:

 

                                (8)

This representation may seem a bit arbitrary, at first, but it emerges rather strongly from careful consideration of the difficulty of sharing communications between decision blocks, and of the limitations of possible alternatives [1]. This is a strong theoretical prediction -- that explicit images of goals or of desired states of the world play a central role in the effectiveness of human planning. Perhaps the word “goal” really is another one of those four-letter words representing a hard-wired invariant of human thought.

                Within each decision block, as before, there is also a need to adapt local critic networks, representing the JA0 and JAI of equation 7. Another network JA+ can improve the accuracy, in principle, of the interface between this block and its successors; however, it is not strictly necessary. Yet another network JA- is needed to help decision block A to formulate the goals gA- which it could pass back to the previous decision blocks.

                Another key feature of this design is the need for a kind of decision network within each block, analogous to the action network of Figure 3. At this level, however, the concern about local optima and the need for exploration of alternatives is very great; therefore, the decision networks must be stochastic networks, which propose possible decisions, based on some notion of their expected payoffs. A key part of the new design [1] is an approach to training such stochastic networks, which tries to make them output

options based on a Gibbs function of their expected value (in effect, J). This function includes a kind of global “temperature” parameter, which is compatible with discussions by Levine and Leven [32], among others, of global variations in novelty-seeking behavior in humans and other organisms. The assumption here is that the neocortex outputs these possible options, but that the discrete go/no-go choices are made in the basal ganglia (except for “decisions” output directly from the motor cortex to the lower brain). This is also consistent with Grossberg’s view that data on the basal ganglia imply that discrete, binary go/no-go decissions are made in that part of the brain. The local critics provide a basis for making these final choices, as a function of the global “temperature.”

                Finally, the decision blocks must each contain a kind of internal Model, similar in a way to the Model network of Figure 3. This can be useful as part of the system to adapt the other networks, as in Figure 3. But it provides another important capability: the capability to simulate possible decisions and results. This capability for simulation or imagination or “dreaming”[22] is crucial to actually exploiting the benefits of large-scale temporal chunking. If a decision block represents a task which takes T time periods to unfold, then it should be possible to consider T alternative possible decisions or tasks or scenarios during a period when only one actual task is accomplished! In the brain, the multiplexing of different decision levels may reduce this benefit somewhat, but one would still expect that more time is spent considering future possibilities than in tracking present reality.

                Another crucial aspect of this design is that the Model within a higher-level decision block must be truly stochastic, like the SEDP design in [7, ch.13]. The reasons for this are discussed further in  [1],

along with the details of how to adapt these various component networks.

 

References

 

[1]P.Werbos, A Brain-Like Design To Learn Optimal Decision Strategies in Complex Environments,

                in M.Karny, K.Warwick and V.Kurkova, eds, Dealing with Complexity: A Neural Networks              Approach. Springer, London, 1997.

[2] P.Werbos, The Roots of Backpropagation: From Ordered Derivatives to Neural Networks and Political                Forecasting, Wiley, 1994.

[3] K.Pribram, ed., Learning as Self-Organization , Erlbaum 1996.

[4] K.Pribram, ed., Origins: Brain and Self-Organization, Erlbaum, 1994, p.46-52.

[5] P.Werbos, Optimization: A Foundation for understanding consciousness. In D.Levine & W. Elsberry        (eds) Optimality in Biological and Artificial Networks?, Erlbaum, 1996.

[6] Bitterman ME 1965 The evolution of intelligence Scientific American January

[7] . D.White & D.Sofge, eds, Handbook of Intelligent Control, Van Nostrand, 1992.

[8] P.Werbos, Optimal neurocontrol: Practical benefits, new results and biological evidence, Proc. World        Cong. on Neural Networks(WCNN95),Erlbaum, 1995

[9]  Proc. Int’l Conf. Neural Networks (ICNN97), IEEE, 1977.

[10] P. Werbos, Neurocontrollers, in  J.Webster, ed, Encyclopedia of Electronics and Electrical Engineering,             Wiley, forthcoming.

[11] P.Werbos, The elements of intelligence. Cybernetica (Namur), No.3, 1968.

[12] W.Nauta & M.Feirtag, Fundamental Neuro-anatomy, W.H.Freeman, 1986.

[13] J.Von Neumann and O.Morgenstern, The Theory of Games and Economic Behavior,Princeton NJ:           Princeton U. Press, 1953.

[14] P.Werbos, The cytoskeleton: Why it may be crucial to human learning and to neurocontrol,       Nanobiology, Vol. 1, No.1, 1992.

[15] Miller GA Galanter EH and Pribram K 1960 Plans and the Structure of Behavior (New York: Holt,              Rinehart and Winston)

[16] Vernon Brooks, The Neural Basis of Motor Control, Oxford U. Press, 198_.

[17] D.O.Hebb, The Organization of Behavior, Wiley, 1949.

[18] A.Barto, R.Sutton and C.Anderson, Neuronlike adaptive elements that can solve difficult learning            control problems, IEEE Trans. SMC, Vol. 13, No.5, 1983, p.834-846.

[19] B.Widrow, N.Gupta & S.Maitra, Punish/reward: learning with a Critic in adaptive threshold systems,        IEEE Trans. SMC, 1973, Vol. 5, p.455-465.

[20] P.Werbos, Advanced forecasting for global crisis warning and models of intelligence, General Systems Yearbook, 1977 issue.

[21] T.Landelius, Reinforcement Learning and Distributed Local Model Synthesis, Ph.D. thesis and Report

                No.469, Department of Electrical Engineering, Linkoping U., 58183, Linkoping, Sweden.

[22] P.Werbos, Building and understanding adaptive systems: A statistical/numerical approach to factory     automation and brain research, IEEE Trans. SMC, Jan./Feb. 1987.

.[23] P.Werbos and A.Pellionisz, Neurocontrol and neurobiology, Proc. Int’l Joint Conf.    Neural   Networks (IJCNN92), IEEE, 1992.

[24] P.Werbos & X.Z.Pang, Generalized maze navigation: SRN critics solve what feedforward or Hebbian        nets cannot.Proc. Conf. Systems, Man and Cybernetics (SMC) (Beijing), IEEE, 1996. (An earlier   version appeared in WCNN96.)

[25] X.Z.Pang & P.Werbos, Neural network design for J function approximation in dynamic                programming, Math. Modelling and Scientific Computing (a Principia Scientia      journal), special    issue on neural nets planned for circa December 1996. See also links on                 www.glue.umd.edu/~pangxz

[26] J.Houk, J.Davis & D.Beiser (eds), Models of Information Processing in the Basal Ganglia, MIT Press,   1995.

[27] W.T.Miller, R.Sutton & P.Werbos (eds), Neural Networks for Control, MIT Press,1990, now in paper

[28] P.Werbos, Consistency of HDP applied to a simple reinforcement learning problem,     Neural   Networks, March 1990

[29] J.Albus, Outline of  Intelligence, IEEE Trans. Systems, Man and Cybernetics, Vol.21, No.2, 1991.

[30] R.Howard, Dynamic Programming and Markhov Processes, MIT Press, 1960.

[31] D.Bertsekas, Dynamic Programming and Optimal Control, Belmont, MA: Athena       Scientific, 1995.

[32] D.S.Levine and S.J.Leven, eds, Motivation, Emotion, and Gvoal Direction in Neural Networks,              Erlbaum, 1992